- Autors Jason Gerald [email protected].
- Public 2024-01-15 08:19.
- Pēdējoreiz modificēts 2025-01-23 12:26.
Frakcijas dalīšana ar daļu var šķist mulsinoša, bet patiesībā tas ir ļoti vienkārši. Viss, kas jums jādara, ir uzsist, pavairot un vienkāršot! Šis raksts jums parādīs procesu un parādīs, cik viegli ir sadalīt daļu ar daļu.
Solis
1. daļa no 2: Izpratne par to, kā sadalīt frakcijas pēc daļām
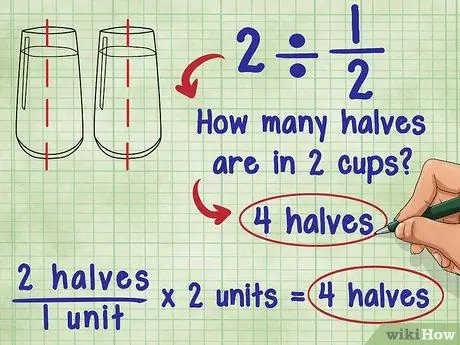
1. solis. Padomājiet par to, ko nozīmē dalīšana ar daļu
Par 2 ÷ 1/2 jautāja Ada: "Cik puse ir 2?" Atbilde ir 4, jo katra vienība (1) sastāv no divām “pusēm” un kopā ir 2 vienības: 2 “puse”/1 vienība * 2 vienības = 4 “puse”.
- Mēģiniet iedomāties to pašu vienādojumu, izmantojot glāzi ūdens: Cik ar pusi glāzes ūdens ir 2 glāzēs ūdens? Katrā glāzē ūdens varat ielej 2 ar pusi tases ūdens. Tas nozīmē, ka būtībā jūs pievienojat “pusi” ūdens glāzes, un jums ir divas glāzes: 2 “puse”/1 tase * 2 tases = 4 “puse”.
- Tas nozīmē, ka, ja dalāmā daļa ir no 0 līdz 1, atbilde vienmēr ir lielāka par sākotnējo skaitli! Tas ir taisnība, ja veselu skaitli vai daļu dala ar daļu.

Solis 2. Saprotiet, ka dalīšana ir pretēja reizināšanai
Tādējādi dalīšanu ar daļu var atrisināt, reizinot ar daļskaitli. Frakcijas atgriezeniskā saite (saukta arī par “reizināšanas apgriezto”) ir daļa, kas ir apgriezta, lai skaitītājs un saucējs apmainītos vietām. Pēc brīža mēs sadalīsim frakcijas ar daļām, nosakot otrās frakcijas savstarpējo vērtību un reizinot abas frakcijas. Tomēr vispirms apskatīsim dažus pretstatus:
- Savstarpējais 3/4 ir 4/3.
- 7/5 pretstats ir 5/7.
- Atgriezeniskā vērtība 1/2 ir 2/1 vai 2.
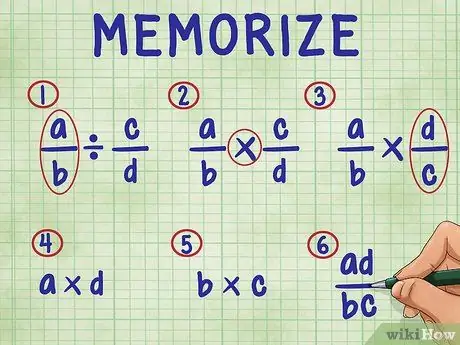
3. solis. Atcerieties šādas darbības, lai dalītu daļu ar daļu
Lai secīgi, soļi ietver:
- Vienkārši atstājiet vienādojuma pirmo daļu.
- Mainiet dalīšanas zīmi uz reizināšanas zīmi.
- Apgrieziet otro daļu (atrodiet tās savstarpējo).
- Reiziniet abu frakciju skaitītāju (augšējo skaitli). Reizināšanas rezultāts ir jūsu atbildes skaitītājs (augšpusē).
- Reiziniet abu frakciju saucēju (apakšējo skaitli). Produkta produkts ir jūsu atbildes saucējs.
- Vienkāršojiet savas daļas, vienkāršojot tās līdz vienkāršākajiem vārdiem.
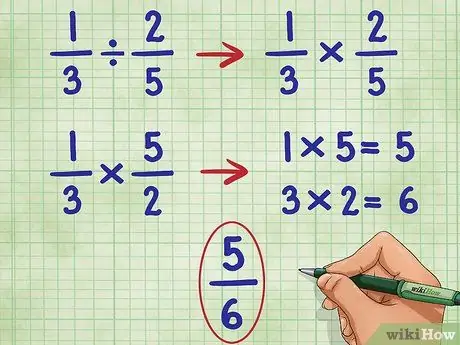
4. solis. Veiciet šīs darbības 1/3 2/5 piemērā
Sāksim, atstājot pirmo daļu un pārvēršot dalīšanas zīmi par reizināšanas zīmi:
- 1/3 ÷ 2/5 = Kļūst:
- 1/3 * _ =
- Tagad mēs mainām otro daļu (2/5), lai atrastu tās savstarpējo vērtību, kas ir 5/2:
- 1/3 * 5/2 =
- Tagad reiziniet abu frakciju skaitītāju (augšējo skaitli), 1*5 = 5.
- 1/3 * 5/2 = 5/
- Tagad reiziniet abu frakciju saucēju (apakšējo skaitli), 3*2 = 6.
- Tagad mums ir: 1/3 * 5/2 = 5/6
- Šo daļu vairs nevar vienkāršot, tāpēc mums ir sava atbilde.

5. solis. Mēģiniet atcerēties šādas atskaņas, lai palīdzētu jums atcerēties:
"Frakciju dalīšana ir vienkārša, apgrieziet otro frakciju un pēc tam reiziniet. Neaizmirstiet vienkāršot, pirms pienācis laiks ēst."
Citā noderīgā atgādinājuma palīdzībā ir norādīts, ko darīt ar katru vienādojuma daļu: “Ļaujiet man (pirmā daļa), mainiet mani (dalījuma zīme), apgrieziet mani (otrā daļa).”
2. daļa no 2: Frakciju dalīšana ar daļām problēmās
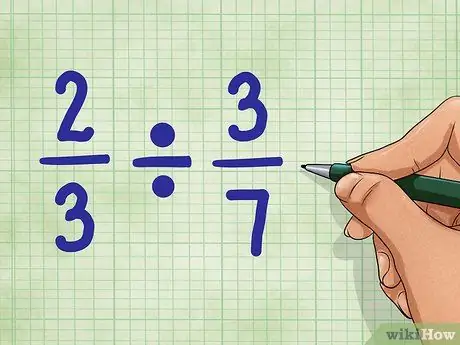
1. solis. Sāciet ar jautājumu paraugiem
Izmantosim 2/3 ÷ 3/7. Šis jautājums prasa daļu skaitu, kas vienāds ar 3/7, kas atrodams 2/3 vērtībā. Neuztraucies. Tas nav tik grūti, kā izklausās!
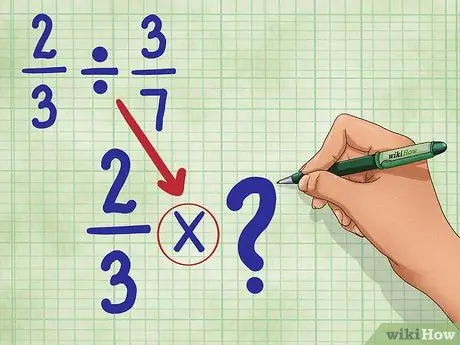
Solis 2. Pārveidojiet dalīšanas zīmi par reizināšanas zīmi
Jūsu jaunais vienādojums būs šāds: 2/3 * _ (Pēc brīža mēs aizpildīsim šo tukšo vietu.)
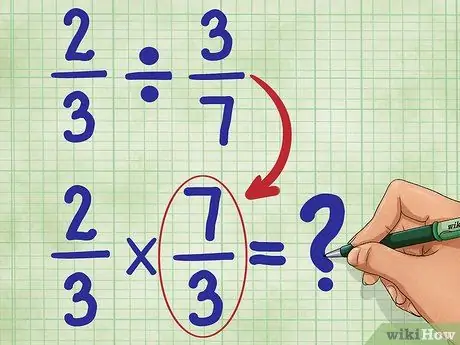
Solis 3. Tagad atrodiet otrās frakcijas savstarpējo vērtību
Tas nozīmē pagriezt 3/7 tā, lai skaitītājs (3) tagad būtu apakšā, un saucējs (7) tagad būtu augšpusē. Savstarpīgums 3/7 ir 7/3. Tagad uzrakstiet savu jauno vienādojumu:
2/3 * 7/3 = _

Solis 4. Reiziniet savas frakcijas
Vispirms reiziniet abu frakciju skaitītājus: 2 * 7 = 14. 14 ir jūsu atbildes skaitītājs (augšējais numurs). Pēc tam reiziniet abu frakciju saucējus: 3 * 3 = 9. 9 ir jūsu atbildes saucējs (apakšējais skaitlis). Tagad jūs to zināt 2/3 * 7/3 = 14/9.
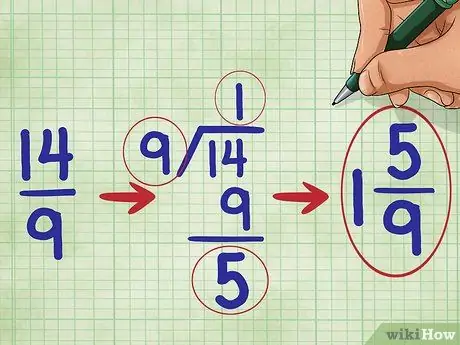
Solis 5. Vienkāršojiet savu frakciju
Šajā uzdevumā, tā kā frakcijas skaitītājs ir lielāks par saucēju, mēs zinām, ka mūsu daļa ir lielāka par 1. Mums tā jāpārvērš par jauktu skaitli. (Jaukts skaitlis ir vesels skaitlis un tā daļa, piemēram, 1 2/3.)
-
Vispirms sadaliet skaitītāju
14. darbība. ar 9.
Skaitlis 14 dalīts ar 9 ir vienāds ar vienu ar atlikušo 5, tāpēc jums vajadzētu pierakstīt savu vienkāršoto daļu šādi: 1 5/9 (“Viens pieci deviņi”).
- Beidz, tu esi atradis atbildi! Varat norādīt, ka jūs vairs nevarat vienkāršot daļu, jo saucējs nav dalāms ar skaitītāju (9 nav dalāms ar 5) un skaitītājs ir pirmskaitlis vai vesels skaitlis, kas dalās tikai ar vienu un pašu skaitli.
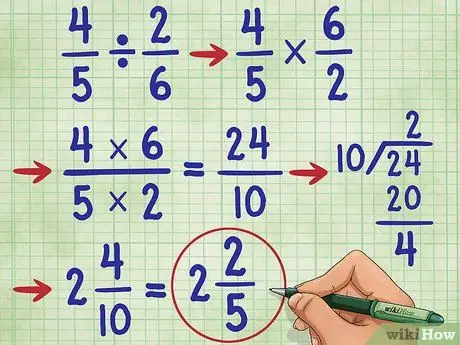
6. solis. Izmēģiniet citu piemēru
Izmēģināsim jautājumu 4/5 ÷ 2/6 =. Vispirms nomainiet dalīšanas zīmi uz reizināšanas zīmi (4/5 * _ =), tad atrodiet reciproku 2/6, kas ir 6/2. Tagad jums ir vienādojums: 4/5 * 6/2 =_. Tagad reiziniet skaitītāju, 4 * 6 = 24, un saucējs 5* 2 = 10. Tagad jums ir 4/5 * 6/2 = 24/10.
Tagad vienkāršojiet daļu. Tā kā skaitītājs ir lielāks par saucēju, šī daļa ir jāpārvērš par jauktu skaitli.
- Vispirms daliet skaitītāju ar saucēju, (24/10 = 2 atlikušie 4).
- Uzrakstiet atbildi kā 2 4/10. Mēs joprojām varam vienkāršot šo daļu vēlreiz!
- Ņemiet vērā, ka 4 un 10 ir pāra skaitļi. Tātad, pirmais solis, lai to vienkāršotu, ir dalīt katru skaitli ar 2. Mēs iegūstam 2/5.
- Tā kā saucējs (5) nav dalāms ar skaitītāju (2) un 5 ir pirmskaitlis, mēs zinām, ka šo daļu vairs nevar vienkāršot. Tātad, mūsu atbilde ir šāda: 2 2/5.

7. solis. Saņemiet papildu palīdzību frakciju vienkāršošanai
Jūs, iespējams, pavadījāt daudz laika, lai uzzinātu, kā vienkāršot frakcijas, pirms mēģināt tās sadalīt viena ar otru. Tomēr, ja jums ir nepieciešama atsvaidzināšana vai cita palīdzība, ir daži lieliski tiešsaistes raksti, kas jums var ļoti palīdzēt.
Saistītie raksti wikiHow
- Kopējo frakciju pārvēršana aiz komata
- Apļa laukuma aprēķināšana
- Polinomu dalīšana, izmantojot sintētisko nodaļu
- Jaukto frakciju sadalīšana






