- Autors Jason Gerald [email protected].
- Public 2024-02-01 14:14.
- Pēdējoreiz modificēts 2025-01-23 12:27.
Viss, kas jums nepieciešams, lai aprēķinātu vidējo ātrumu, ir kopējais pārvietojums. vai pozīcijas maiņa, un kopējais laiks. Atcerieties, ka ātrums aprēķina arī objekta virzienu un ātrumu, tāpēc atbildē iekļaujiet virzienu, piemēram, "ziemeļi", "priekšā" vai "pa kreisi". Ja jūsu ātruma aprēķināšanas problēma ietver arī pastāvīgu paātrinājumu, varat uzzināt ātru veidu, kā vēl vieglāk atrast atbildi.
Solis
1. metode no 2: vidējā pārvietošanās ātruma un laika aprēķināšana

1. solis. Atcerieties, ka ātrums ietver gan objekta ātrumu, gan virzienu
Ātrums raksturo ātrumu, kādā mainās objekta pozīcija. Tas ir saistīts ne tikai ar objekta pārvietošanās ātrumu, bet arī ar tā virzienu. "100 metri sekundē uz dienvidiem" ir atšķirīga ātruma vērtība nekā "100 metri sekundē uz austrumiem".
- Daudzumus, kuriem ir virziens, sauc par vektoru lielumiem”. Šo daudzumu var atšķirt no bezvirziena daudzuma, ko sauc par skalāro daudzumu, uzrakstot bultiņu virs mainīgā. Piemēram, apzīmējums v apzīmē likmi, bet apzīmējums v → apzīmē ātrumu vai ātrumu + virzienu. Šajā rakstā izmantotais apzīmējums v apzīmē ātrumu.
- Zinātnisku problēmu gadījumā attāluma izteikšanai jāizmanto skaitītāji vai citas metriskās vienības, bet ikdienas vajadzībām varat izmantot jebkuru vienību, kas jums patīk.
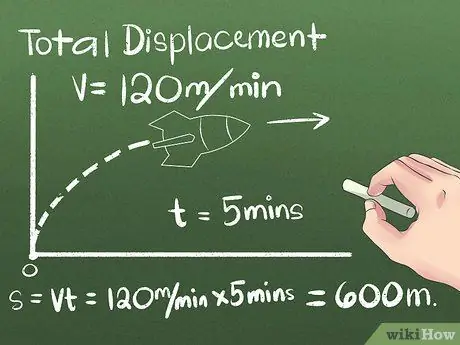
2. solis. Atrodiet kopējo pārvietojuma vērtību
Pārvietojums ir objekta stāvokļa vai attāluma un virziena maiņa starp sākuma un beigu punktiem. Var neņemt vērā virzienu, kurā objekts pārvietojas pirms galīgās pozīcijas sasniegšanas, jo tiek ņemts vērā tikai attālums starp sākuma un beigu punktu. Pirmajā piemērā mēs izmantosim objektu, kas pārvietojas nemainīgā ātrumā vienā virzienā:
- Pieņemsim, ka raķete 5 minūtes virzās uz ziemeļiem ar nemainīgu ātrumu 120 metri minūtē. Lai aprēķinātu galīgo pozīciju, izmantojiet formulu s = vt vai izmantojiet praktisko domāšanu, lai aprēķinātu raķetes nobraukto attālumu pēc tam (5 minūtes) (120 metri minūtē) = 600 metrus uz ziemeļiem no sākuma punkta.
- Problēmas, kas saistītas ar pastāvīgu paātrinājumu, varat tās atrisināt ar s = vt + at2, vai izmantojiet īsu metodi, kas aprakstīta citā sadaļā, lai atrastu atbildi.
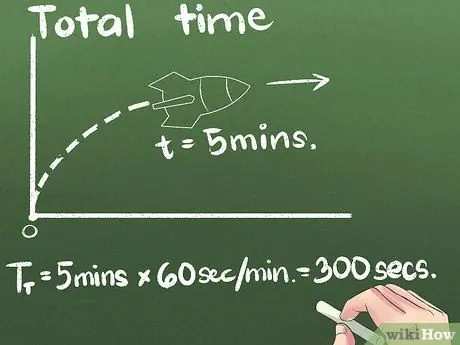
Solis 3. Atrodiet kopējo pavadīto laiku
Mūsu piemērā raķete virzās uz priekšu 5 minūtes. Jūs varat izteikt vidējo ātrumu jebkurā laika vienībā, bet otrā ir starptautiskā zinātniskā standarta vienība. Šajā piemērā mēs mainīsim sekundes vienības: (5 minūtes) x (60 sekundes/minūtē) = 300 sekundes.
Pat zinātnisku problēmu gadījumā, ja jautājumā tiek izmantota stunda vai lielāka laika vienība, vispirms būs vieglāk aprēķināt ātrumu, pēc tam galīgo atbildi pārvērst metros sekundē
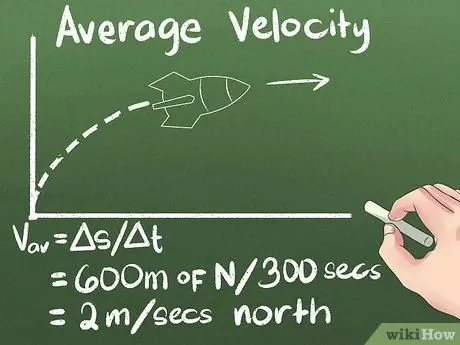
4. solis. Aprēķiniet vidējo ātrumu kā pārvietojumu laika gaitā
Ja jūs zināt, cik tālu objekts pārvietojas un cik ilgs laiks būs vajadzīgs, lai tur nokļūtu, jūs zināt, cik ātri tas pārvietojas. Tātad mūsu izmantotajā piemērā raķetes vidējais ātrums ir (600 metri uz ziemeļiem) / (300 sekundes) = 2 metri sekundē uz ziemeļiem.
- Neaizmirstiet iekļaut virzienu (piemēram, "priekšā" vai "ziemeļos").
- Formulā vvid = s/Δt. Delta simbols nozīmē "pārmaiņas", tātad s/Δt nozīmē "pozīcijas maiņa noteiktā laika periodā".
- Vidējo ātrumu var uzrakstīt kā vvid, vai kā v ar horizontālu līniju virs tā.

Solis 5. Atrisiniet sarežģītākas problēmas
Ja objekts maina virzienu vai ātrumu, nemulsiniet. Vidējais ātrums joprojām tiek "aprēķināts" tikai no kopējā pārvietojuma un kopējā laika. To, kas notiek starp sākuma un beigu punktiem, varat ignorēt. Tālāk ir sniegti daži piemēri objektam, kas pārvietojas ar tādu pašu pārvietojumu un kopējo laiku un līdz ar to vienādu vidējo ātrumu:
-
Anna 2 sekundes iet uz rietumiem ar ātrumu 1 metrs/s, tad pēkšņi paātrinās līdz 3 metriem sekundē un 2 sekundes turpina iet uz rietumiem. Kopējais pārvietojums ir (1 m/s uz rietumiem) (2 sek) + (3 m/s uz rietumiem) (2 sek) = 8 metri uz rietumiem. Kopējais laiks ir 2 sekundes + 2 sekundes = 4 sekundes. Tātad vidējais ātrums ir 8 metri uz rietumiem/ 4 sekundes = 2 metri sekundē uz rietumiem.
- Bārts 3 sekundes iet uz rietumiem ar ātrumu 5 metri sekundē, pēc tam pagriežas un 1 sekundi soļo uz austrumiem ar ātrumu 7 metri sekundē. Mēs varam domāt par kustību austrumu virzienā kā "negatīvu kustību uz rietumiem", tāpēc kopējais pārvietojums ir = (5 metri/sek uz rietumiem) (3 sekundes) + (-7 m/s uz rietumiem) (1 sek) = 8 metri. Kopējais laiks = 4 sekundes. Vidējais ātrums = 8 metri uz rietumiem / 4 sekundes = 2 metri sekundē uz rietumiem.
-
Šarlote gāja uz ziemeļiem 1 metru un tad gāja uz rietumiem 8 metrus, tad uz dienvidiem 1 metru. Visa brauciena veikšanai nepieciešamais laiks ir 4 sekundes. Uzzīmējiet diagrammu uz papīra lapas, un jūs redzēsit, ka beigu punkts atrodas 8 metrus uz rietumiem no sākuma punkta, tāpēc šī vērtība ir pārvietojums. Kopējais laiks, kas nepieciešams, ir 4 sekundes, tātad vidējais ātrums ir 8 metri uz rietumiem / 4 sekundes = 2 metri sekundē uz rietumiem.
2. metode no 2: fiksētā paātrinājuma vidējā ātruma aprēķināšana

Solis 1. Apsveriet sākotnējo ātrumu un pastāvīgu paātrinājumu
Pieņemsim, ka mūsu problēma ir šāda: "Velosipēds pārvietojas pa labi ar ātrumu 5 m/s ar nemainīgu paātrinājumu 2 m/s2. Ja šis velosipēds kustas 5 sekundes, kāds ir tā vidējais ātrums?"
Ja vienība "metrs/sekundē2"lai jūs sajauktu, uzrakstiet to kā" metri sekundē/sekundē "vai" metri sekundē sekundē. "Paātrinājums 2 metri sekundē nozīmē, ka ātrums palielinās par 2 metriem sekundē.

2. solis. Izmantojiet paātrinājumu, lai atrastu galīgo ātrumu
Paātrinājums, kas apzīmēts ar apzīmējumu a, ir ātruma (vai ātruma) izmaiņu ātrums. Ātrums palielinās ar nemainīgu pieauguma tempu. Izmantojot paātrinājumu, varat uzzīmēt tabulu, lai atrastu ātrumu dažādos velosipēda brauciena laikos. Mums ir jāizveido šī tabula, lai atrastu problēmas beigu punktu (t = 5 sekundes), bet mēs izveidosim garāku tabulu, lai jums būtu vieglāk saprast šo jēdzienu:
- Sākuma punktā (laiks t = 0 sekundes) velosipēds pārvietojas ar ātrumu 5 metri/s.
- Pēc 1 sekundes (t = 1) velosipēds pārvietojas ar ātrumu 5 metri sekundē + pie = 5 metri sekundē + (2 metri sekundē)2) (1 sekunde) = 7 metri sekundē.
- Pie t = 2 velosipēds pārvietojas pa labi ar ātrumu 5+ (2) (2) = 9 metri/sek.
- Pie t = 3 velosipēds pārvietojas pa labi ar ātrumu 5+ (2) (3) = 11 metri/sek.
- Pie t = 4 velosipēds pārvietojas pa labi ar ātrumu 5+ (2) (4) = 13 metri/sek.
- Pie t = 5 velosipēds pārvietojas pa labi ar ātrumu 5+ (2) (5) = 15 metri sekundē.

3. solis. Izmantojiet šo formulu, lai atrastu vidējo ātrumu
Ja un "tikai", ja paātrinājums ir nemainīgs, vidējais ātrums būs vienāds ar galīgā un sākotnējā ātruma summas vidējo vērtību. (vf +vi)/2. Iepriekš minētajai mūsu piemēra problēmai velosipēda sākotnējais ātrums ir vi 5 metri sekundē. Pēc aprēķināšanas galīgais ātrums ir vf 15 metri sekundē. Saskaitot šīs divas vērtības, mēs iegūstam (15 metri sekundē + 5 metri sekundē)/2 = (20 metri sekundē)/2 = 10 metri sekundē pareizajā virzienā.
- Neaizmirstiet iekļaut virzienu, šajā gadījumā "pareizi".
- Šo terminu var uzrakstīt kā v0 (ātrums laikā 0 vai sākotnējais ātrums) un v (galīgais ātrums).

Solis 4. Intuitīvi izprast vidējā ātruma formulu
Lai atrastu vidējo ātrumu, mēs varam izmantot ātrumu jebkurā vietā un atrast vidējo ātrumu visiem. (Šī ir vidējā definīcija.) Tā kā tas prasa aprēķinus vai bezgalīgu laiku, saprotiet šo formulu intuitīvāk. Tā vietā, lai izmantotu katru reizi, aprēķiniet abu laika punktu vidējo ātrumu un skatiet rezultātus. Viens brīdis ir tuvu brauciena sākumam, kur velosipēds dodas lēni, un vēl viens punkts atrodas netālu no gala punkta, kur velosipēds brauc ātri.

Solis 5. Pārbaudiet intuitīvo teoriju
Izmantojiet iepriekš minēto tabulu, lai noteiktu ātrumu dažādos laika punktos. Daži pāri, kas atbilst mūsu kritērijiem, ir (t = 0, t = 5), (t = 1, t = 4) vai (t = 2, t = 3). Ja vēlaties, varat pārbaudīt šo formulu ar t vērtībām, kas nav veseli skaitļi.
Neatkarīgi no izvēlētā punktu pāra vidējais ātrums tajā laikā vienmēr būs vienāds. Piemēram, ((5+15)/2), ((7+13)/2) vai ((9+11)/2) visi vienādi 10 metri sekundē pa labi

6. Pabeigt intuitīvo skaidrojumu
Ja mēs izmantosim šo metodi ar katras veiktās reizes sarakstu, mēs turpināsim aprēķināt ceļojuma pirmās puses un ceļojuma otrās puses vidējo. Katras pusītes segšanai nepieciešamais laiks ir vienāds, tāpēc, pabeidzot skaitīšanu, netiek zaudēts ātrums.
- Tā kā abi pāri sniegs vienādu rezultātu, arī šo ātrumu vidējā vērtība būs vienāda. Mūsu piemērā visa ātrums "10 metri sekundē pa labi" joprojām būs 10 metri sekundē pa labi.
- Mēs varam atrast šo vērtību, aprēķinot jebkura pāra vidējo vērtību, piemēram, sākotnējo un beigu ātrumu. Mūsu piemērā šie ātrumi tiek sasniegti pie t = 0 un t = 5, un tos var aprēķināt, izmantojot iepriekš minēto formulu: (5+15)/2 = 10 metri/s pa labi.

Solis 7. Izprotiet šo formulu matemātiski
Ja jums patīk pierādījumi, kas pierakstīti kā formulas, varat sākt ar formulu, lai aprēķinātu nobraukto attālumu, pieņemot nemainīgu paātrinājumu, un no turienes iegūt formulu:
- s = vit + plkst2. (Tehniski s un t, vai pozīcijas maiņa un laika maiņa, bet jūs arī saprastu, ja uzrakstītu s un t.)
- Vidējais ātrums vvid definēts kā s/t, tāpēc ievadiet formulu formā s/t.
- vvid = s/t = vi + plkst
- Paātrinājums x laiks ir vienāds ar kopējā ātruma izmaiņām vai vf - vi. Tātad mēs varam formulā aizstāt “at” un iegūt:
- vvid = vi + (vf - vi).
- Vienkāršojiet: vvid = vi + vf - vi = vi + vf = (vf +vi)/2.
Padomi
- Ātrums atšķiras no ātruma, jo ātrums ir vektora lielums, turpretī ātrums ir skalārs lielums. Vektoru daudzumi ietver gan virzienu, gan lielumu, savukārt skalārie daudzumi ietver tikai lielumu.
- Ja objekts pārvietojas vienā dimensijā, piemēram, pa kreisi-pa labi, varat izmantot pozitīvu skaitli, lai attēlotu vienu virzienu (piemēram, pa labi), un negatīvu skaitli, lai attēlotu citu virzienu (pa kreisi). Uzrakstiet šo apzīmējumu lapas augšpusē, lai tas būtu skaidrs cilvēkiem, kas lasa jūsu darbu.






