Vidējais svērtais, kas pazīstams arī kā vidējais svērtais, ir nedaudz sarežģītāks nekā parastais vidējais aritmētiskais. Kā norāda nosaukums, vidējais svērtais ir tad, kad izstrādātajiem skaitļiem ir vērtības vai svari, kas ir savstarpēji saistīti. Piemēram, mēs iesakām izmantot vidējo svērto vērtību, ja vēlaties aprēķināt kopējo atzīmi kursā, kuram katram uzdevumam ir svērtais procents. Izmantotā procedūra būs nedaudz atšķirīga atkarībā no tā, vai kopējais svars ir 1 (vai 100%) vai nē.
Solis
1. metode no 2: vidējā svērtā aprēķināšana, ja kopējais svars ir 1
1. solis. Apkopojiet skaitļus, kurus vēlaties aprēķināt vidēji
Jums jāsāk, uzskaitot numurus, ar kuriem vēlaties strādāt. Piemēram, ja vēlaties klasē novērtēt atzīmju vidējo svērto vērtību, vispirms pierakstiet tās sarakstā.
Piemēram, sakiet, ka kursā jūsu kopējais punktu skaits ir 82 par viktorīnām, 90 par eksāmeniem un 76 par papīra uzdevumiem
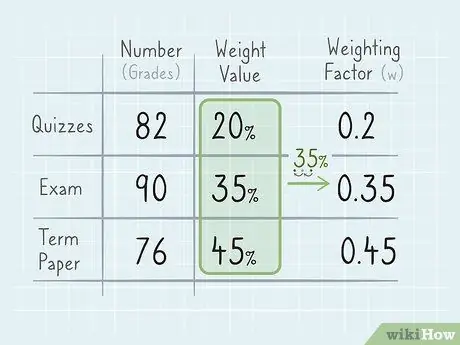
2. solis. Nosakiet katra skaitļa svērto vērtību
Kad esat sagatavojis visus skaitļus, jums jāzina to attiecīgais svars kā daļa no galīgā vidējā. Piemēram, saistītos kursos viktorīnas sver 20% no kopējā punktu skaita, bet eksāmeni - 35%, un darbi - 45%. Šajā gadījumā kopējais svaru skaits ir 1 (vai 100%).
Lai aprēķinos varētu izmantot procentus, tie jāpārvērš decimāldaļās. Rezultātu sauc par "svēršanas koeficientu"
Padoms:
Procentus var viegli pārvērst decimāldaļās! Vienkārši pabīdiet aiz komata divus ciparus pa kreisi no skaitļa. Piemēram, 75% pārvēršas par 0,75.
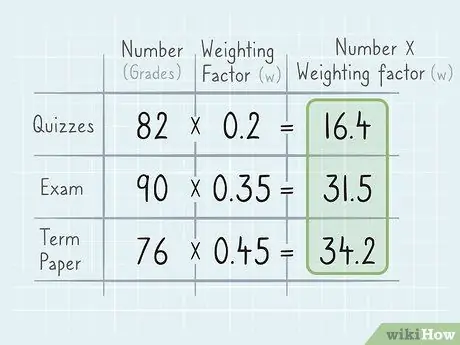
Solis 3. Reiziniet katru skaitli ar tā svēršanas koeficientu (w)
Kad esat ieguvis visus skaitļus, saskaņojiet katru skaitli (x) ar tā svēršanas koeficientu (w). Jūs reizināsit katru skaitļu un svaru kopu, pēc tam saskaitīsit visus rezultātus, lai atrastu vidējo.
Piemēram, ja jūsu viktorīnas kopējais rezultāts ir 82 un viktorīnas svars ir 20%, reiziniet 82 x 0,2. Šajā gadījumā x = 82 un w = 0, 2
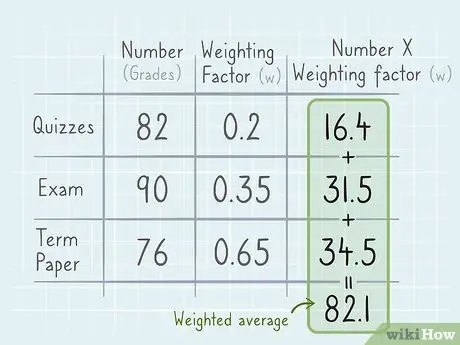
4. solis. Pievienojiet visus produktus, lai atrastu vidējo svērto vērtību
Pamatformula vidējam svērtajam, kura kopējais svars ir 1, ir x1 (w1) + x2 (w2) + x3 (w3) utt., Kur x ir katrs kopas skaitlis un w ir atbilstošais svēruma koeficients. Lai atrastu vidējo svērto vērtību, vienkārši reiziniet katru vērtību ar tās svēruma koeficientu un saskaitiet visus rezultātus. Kā piemērs:
Viktorīnu, eksāmenu un darbu vidējie svērtie rezultāti ir šādi: 82 (0, 2) + 90 (0, 35) + 76 (0, 45) = 16, 4 + 31, 5 + 34, 2 = 82, 1. Tas ir, jums ir 82,1% rādītājs saistītajā priekšmetā
2. metode no 2: vidējā svērtā aprēķināšana, ja kopējais svars nav vienāds 1
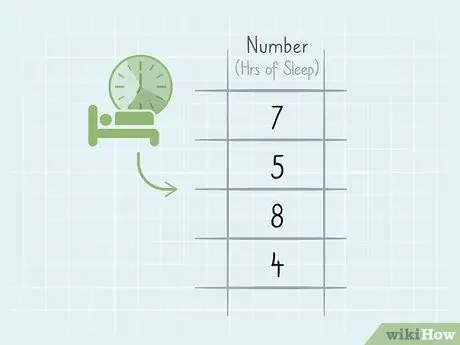
1. solis. Pierakstiet skaitļus, kurus vēlaties aprēķināt vidēji
Aprēķinot vidējo svērto vērtību, kopējais svars ne vienmēr ir vienāds ar 1 (vai 100%). Jebkurā gadījumā sāciet apkopot datus, lai varētu aprēķināt vidējo.
Piemēram, varbūt vēlaties aprēķināt vidējo miega laiku katru nakti 15 nedēļu laikā. Katru dienu miega laiks var mainīties, piemēram, 5, 8, 4 vai 7 stundas naktī
2. solis. Atrodiet svēruma koeficientu katram skaitlim
Kad visi numuri ir savākti, atrodiet kopējo svaru, kas saistīts ar katru numuru. Piemēram, pieņemsim, ka 15 nedēļu laikā dažās naktīs guļat vairāk, bet citās mazāk. Šajā gadījumā nedēļu var izmantot kā “svaru”, jo tas atspoguļo vidējo nakšņojumu skaitu, ko jūs nedēļas laikā gulējat. Tādējādi svēršanas faktors ir nedēļu skaits, kas saistīts ar katru miega ilgumu. Piemēram, šeit ir svēršanas faktori un ar tiem saistītie skaitļi lielākajā daļā nedēļu:
- 9 nedēļas, kad jūs vidēji gulējat 7 stundas naktī.
- 3 nedēļas, kad guļ 5 naktī.
- 2 nedēļas, kad jūs guļat 8 stundas naktī.
- 1 nedēļa, kad jūs guļat 4 stundas naktī.
- Nedēļu skaits, kuram atbilst katrs skaitlis, ir jūsu svēršanas faktors. Šajā gadījumā jūs guļat ne vairāk kā 7 stundas naktī lielākajā daļā nedēļu, bet citas nedēļas jūs guļat vairāk vai mazāk.
3. solis. Aprēķiniet kopējo svēršanas koeficientu
Lai varētu noteikt vidējo svērto vērtību, jums ir jāsummē visi svēršanas faktori, lai iegūtu kopējo vērtību. Šajā piemērā mēs redzējām, ka kopējais svēruma koeficients ir 15, jo jūs novērojat miega modeļus 15 nedēļu laikā.
Kopējais nedēļu skaits ir šāds: 3 nedēļas + 2 nedēļas + 1 nedēļa + 9 nedēļas = 15 nedēļas
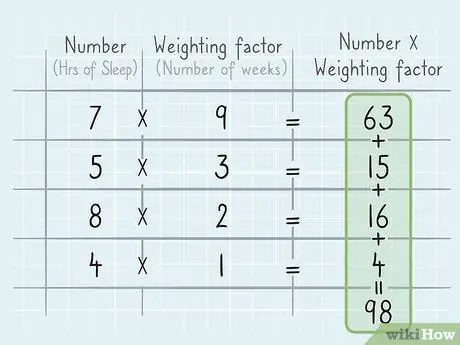
Solis 4. Reiziniet katru skaitli ar tā svēršanas koeficientu un saskaitiet rezultātus
Tālāk jums jāreizina katrs skaitlis datos ar attiecīgo svēruma koeficientu, tāpat kā aprēķinot datus, kuru kopējais svars ir 1 vai 100%. Ja tā, sasummējiet rezultātus. Piemēram, ja jūs aprēķināt miega stundas 15 nedēļu laikā, reiziniet vidējās miega stundas ar atbilstošo nedēļu skaitu. Tu saņemsi:
5 stundas naktī (3 nedēļas) + 8 stundas naktī (2 nedēļas) + 4 stundas naktī (1 nedēļa) + 7 stundas naktī (9 nedēļas) = 5 (3) + 8 (2) + 4 (1) + 7 (9) = 15 + 16 + 4 + 63 = 98
Solis 5. Sadaliet iepriekšminētā aprēķina rezultātu ar svaru summu, lai atrastu vidējo
Pēc skaitļa reizināšanas ar atbilstošo svēruma koeficientu, pēc tam rezultātu sasummēšanu, daliet ar svaru skaitu, lai iegūtu vidējo svērto vērtību. Kā piemērs:
