Vai jūs nezināt, kā uzzīmēt lineāros vienādojumus, neizmantojot kalkulatoru? Par laimi, lineāro vienādojumu attēlošana ir diezgan vienkārša, ja zināt, kā to izdarīt. Viss, kas jums jādara, ir saprast dažas lietas par savu vienādojumu, un jūs varēsit to izdarīt. Sāksim.
Solis
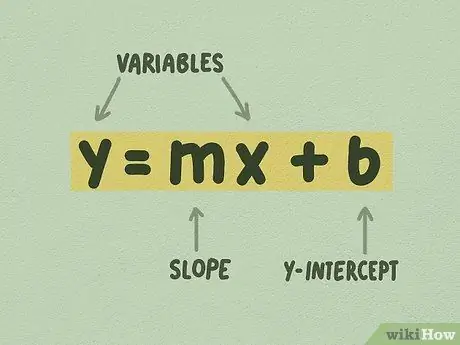
1. solis. Pārliecinieties, vai lineārajam vienādojumam ir forma y = mx + b
Šo formu sauc par y-pārtveršanas formu, un tā, iespējams, ir vieglākā forma, ko izmantot lineāro vienādojumu grafikā. Vienādojuma vērtībai nav jābūt veselam skaitlim. Bieži vien jūs redzēsit vienādojumu, kas izskatās šādi: y = 1/4x + 5, kur 1/4 ir m un 5 ir b.
- m sauc par "slīpumu" vai dažreiz par "gradientu". Slīpums tiek definēts kā palielinājums pāri sānam vai izmaiņas y dalītas ar x izmaiņām.
- b ir definēts kā "y-pārtveršana". Y krustojums ir punkts, kurā līnija krustojas ar Y asi.
- x un y ir mainīgie. Jūs varat atrisināt noteiktu x vērtību, piemēram, ja jums ir punkts y un jūs zināt m un b vērtības. Tomēr x, nekad nav tikai viena vērtība: tā vērtība mainās, kad līnija iet uz augšu vai uz leju.
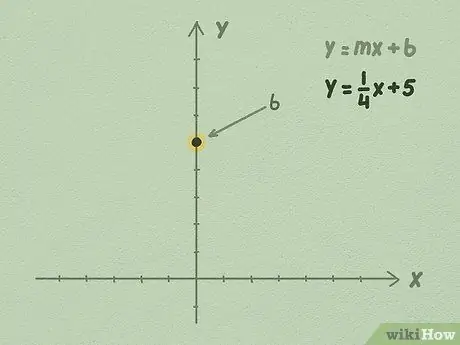
Solis 2. Uzzīmējiet skaitli b uz Y ass
Jūsu b vērtība vienmēr būs racionāls skaitlis. Neatkarīgi no skaitļa b, atrodiet tā vērtību uz Y ass un novietojiet to vertikālās ass punktā.
Piemēram, izmantosim vienādojumu y = 1/4x + 5. Tā kā pēdējais skaitlis ir b, mēs zinām, ka b ir vienāds ar 5. Virzieties uz augšu par 5 punktiem uz Y ass un atzīmējiet punktus. Šeit jūsu taisne krustojas ar Y asi
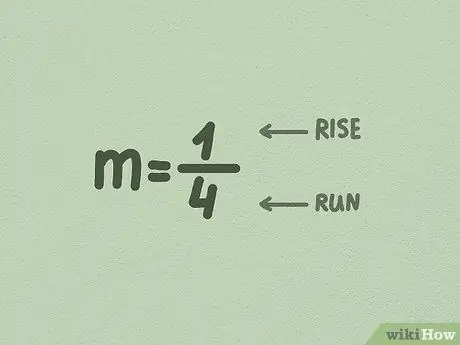
Solis 3. Pārveidojiet m par daļu
Bieži vien skaitlis x priekšā jau ir daļiņa, tāpēc jums tas nav jāmaina. Bet, ja nē, vienkārši mainiet to, ievietojot m vērtību zem skaitļa 1.
- Pirmais skaitlis (skaitītājs) ir pieauguma pieaugums, dalīts ar malu. Šis skaitlis norāda, cik tālu līnija iet uz augšu vai vertikāli.
- Otrais skaitlis (saucējs) ir puse augošā virzienā, dalīta ar malu. Šis skaitlis norāda, cik tālu līnija pārvietojas uz sāniem vai horizontāli.
- Piemēram:
- Slīpums 4/1 pārvieto par 4 punktiem uz augšu par katru 1 punktu uz sāniem.
- Slīpums -2/1 pārvietojas par 2 punktiem uz leju par katru 1 punktu uz sāniem.
- Slīpums 1/5 pārvietojas par 1 punktu uz augšu par katriem 5 punktiem uz sāniem.
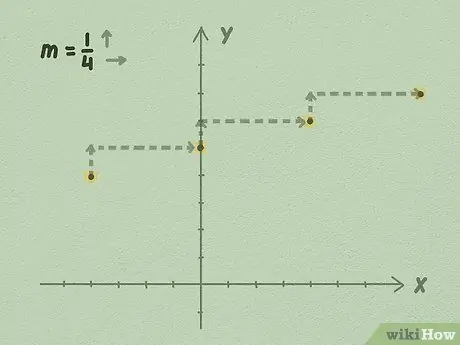
4. solis. Sāciet līnijas pagarināšanu no b, izmantojot slīpumu, vai uz augšu, dalot ar sānu
Sāciet ar savu b vērtību: mēs zinām, ka vienādojums pārsniedz šo punktu. Paplašiniet līniju, ņemot jūsu slīpumu un izmantojot tās vērtību, lai iegūtu vienādojuma punktus.
- Piemēram, izmantojot iepriekš redzamo ilustrāciju, jūs varat redzēt, ka par katru 1 punktu uz augšu līnija pārvietojas par 4 punktiem pa labi. Tas notiek tāpēc, ka līnijas slīpums ir 1/4. Jūs pagarināt līniju uz nenoteiktu laiku uz abām pusēm, turpinot izlietot līdz pusei, lai attēlotu līniju.
- Slīpums ir pozitīvs, pārvietojoties uz augšu, bet slīpums ir negatīvs, pārvietojoties lejup. Piemēram, slīpums -1/4 pārvietosies uz leju par 1 punktu par katru 4 punktu uz sāniem.
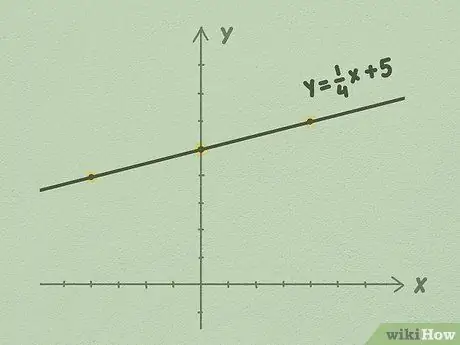
5. solis. Turpiniet līnijas pagarināšanu, izmantojot lineālu un pārliecinieties, ka kā vadlīniju izmantojat slīpumu m
Pagariniet līniju uz nenoteiktu laiku, un esat pabeidzis grafiski attēlot savu lineāro vienādojumu. Diezgan viegli, vai ne?
