Izmantojot Spīrmena ranga korelācijas koeficientu, mēs varam noteikt, vai diviem mainīgajiem ir monotoniska funkciju saistība (tas ir, palielinoties vienam skaitlim, palielināsies arī otrs skaitlis vai otrādi). Lai aprēķinātu Spīrmena ranga korelācijas koeficientu, jums jāsakārto un jāsalīdzina datu kopas, lai atrastu d2, un pēc tam ievadiet datus standarta vai vienkāršotajā Spīrmena ranga korelācijas koeficienta formulā. Šos koeficientus var aprēķināt arī, izmantojot Excel formulas vai R komandu.
Solis
1. metode no 3: manuāls veids
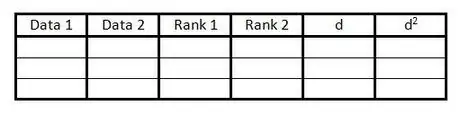
Solis 1. Izveidojiet tabulu
Tabulu izmanto, lai iekļautu visu informāciju, kas nepieciešama, lai aprēķinātu Spīrmena ranga korelācijas koeficientu. Jums ir nepieciešama šāda tabula:
- Izveidojiet 6 kolonnas ar virsrakstiem, kā piemērs.
- Sagatavojiet tik daudz tukšu rindu, cik ir datu pāru.
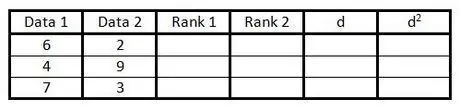
2. solis. Aizpildiet pirmās divas kolonnas ar datu pāriem
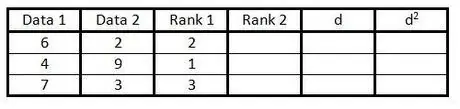
3. solis. Ievadiet datu sleju pirmās slejas rangu trešajā slejā no 1 līdz n (datu skaits)
Sniedziet vērtējumu 1 zemākajai vērtībai, 2 vērtējumu nākamajai zemākajai vērtībai utt.
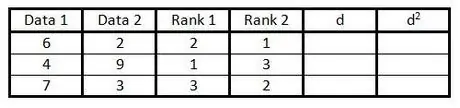
4. solis. Ceturtajā kolonnā rīkojieties tāpat kā 3. darbībā, bet sarindojiet datus otrajā slejā
-
Vidējais_742 Ja ir divi (vai vairāki) dati ar vienādu vērtību, aprēķiniet datu vidējo vērtējumu un pēc tam ievadiet tos tabulā, pamatojoties uz šo vidējo vērtību.
Labajā piemērā vērtējumiem 2 un 3 ir divas vērtības 5. Tā kā ir divi 5, atrodiet vērtējumu vidējo. Vidēji 2 un 3 ir 2,5, tāpēc abām vērtībām 5 ievadiet vērtējuma vērtību 2,5.
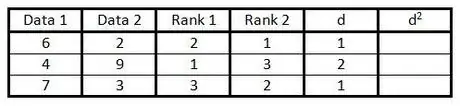
Solis 5. Slejā "d" aprēķiniet starpību starp diviem ranga slejas numuriem
Tas ir, ja viena kolonna ir ierindota 1. vietā, bet otra - 3. vietā, atšķirība ir 2. (zīmei nav nozīmes, jo nākamais solis ir vērtības kvadrāts.)
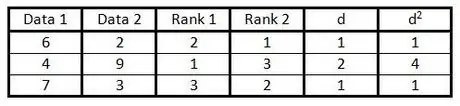
6. solis. Kvadrējiet katru skaitli kolonnā "d" un ierakstiet rezultātu slejā "d2".
7. solis. Pievienojiet visus datus slejā d2".
Rezultāts ir d2.
8. solis. Izvēlieties vienu no šīm formulām:
-
Ja neviens no vērtējumiem nav tāds pats kā iepriekšējā solī, ievadiet šo vērtību vienkāršotajā Spīrmena ranga korelācijas koeficienta formulā
Solis8_271 un aizstājiet "n" ar datu pāru skaitu, lai iegūtu rezultātu.
Step9_402 -
Ja iepriekšējā solī ir līdzīgs rangs, izmantojiet standarta Spīrmena ranga korelācijas koeficienta formulu:
Spearman
9. solis. Interpretējiet rezultātus
Vērtība var svārstīties no -1 līdz 1.
- Ja vērtība ir tuvu -1, korelācija ir negatīva.
- Ja vērtība ir tuvu 0, nav lineāras korelācijas.
- Ja vērtība ir tuvu 1, korelācija ir pozitīva.
2. metode no 3: Excel izmantošana
1. solis. Izveidojiet jaunu sleju datiem kopā ar to rangu
Piemēram, ja jūsu dati atrodas kolonnā A2: A11, izmantojiet formulu "= RANK (A2, A $ 2: A $ 11)" un kopējiet to uz leju, līdz tas aptver visas kolonnas un rindas.
2. solis. Mainiet to pašu vērtējumu, kas aprakstīts 1. metodes 3. un 4. darbībā
3. solis. Jaunajā šūnā aprēķiniet korelāciju starp divām ranga kolonnām ar formulu "= CORREL (C2: C11, D2: D11)"
Šajā piemērā C un D attiecas uz kolonnu, kurā atrodas rangs. Jaunā šūna tiks aizpildīta ar Spīrmena ranga korelāciju.
3. metode no 3: izmantojot R
1. solis. Vispirms instalējiet programmu R, ja jums tā vēl nav
(Skatīt
2. darbība. Saglabājiet savus datus CSV formātā, pirmajās divās kolonnās ievietojiet datus, kuriem vēlaties atrast korelāciju
Mēs to varam izdarīt, izmantojot izvēlni "Saglabāt kā".
3. solis. Atveriet R redaktoru
Ja strādājat no termināļa, vienkārši palaidiet R. Ja strādājat no darbvirsmas, noklikšķiniet uz ikonas R.
4. solis. Ierakstiet šādu komandu:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") un nospiediet taustiņu Enter.
- aktieri (rangs (d [, 1]), rangs (d [, 2]))
Padomi
Datiem jāsastāv vismaz no 5 pāriem, lai varētu redzēt tendenci (datu skaits ir 3 pāri piemērā, lai vienkāršotu aprēķinus)
Brīdinājums
- Spīrmena ranga korelācijas koeficients identificē tikai korelācijas stiprumu, ja dati konsekventi palielinās vai samazinās. Ja datiem ir cita tendence, Spīrmena ranga korelācija Nē sniegs precīzu attēlojumu.
- Šī formula ir balstīta uz pieņēmumu, ka nav vienādu vērtējumu. Ja rangs ir tāds pats kā piemērā, mums vajadzētu izmantot šo definīciju: reizināšanas momenta korelācijas koeficients pēc ranga.
