- Autors Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Pēdējoreiz modificēts 2025-01-23 12:26.
Ja jūs zināt, kā aprēķināt aizdevuma maksājumus, varat plānot savu budžetu, lai vēlāk jūs nepārsteigtu. Ieteicams izmantot tiešsaistes aizdevumu kalkulatoru, jo, veicot aprēķinus, izmantojot parastu kalkulatoru, kurā tiek izmantotas garas formulas, ir vieglāk kļūdīties.
Solis
1. metode no 3: tiešsaistes kalkulatora izmantošana

Solis 1. Atveriet tiešsaistes aizdevuma kalkulatoru
Lapas augšpusē esošajā paraugu sadaļā varat nospiest kalkulatoru, pēc tam atveriet to ar Google disku vai lejupielādējiet, lai to varētu atvērt, izmantojot programmu Excel vai citu programmu. Turklāt atveriet vienu no šīm saitēm:
- Bankrate.com un MLCalc ir vienkārši kalkulatori, kas parāda arī visu jūsu maksājumu grafika tabulu, ieskaitot atlikušo parādu.
- CalculatorSoup ir īpaši noderīgs neparastiem maksājumiem vai palielinātu intervālu izmantošanai. Piemēram, hipotēkas Kanādā parasti tiek pievienotas reizi sešos mēnešos vai divas reizes gadā. (Iepriekš minētajā kalkulatorā tiek pieņemts, ka procenti tiek pievienoti katru mēnesi un maksājumi tiek veikti katru mēnesi.)
- Programmā Excel varat izveidot savu kalkulatoru, līdzīgi kā iepriekš minētajā wikiHow piemērā.
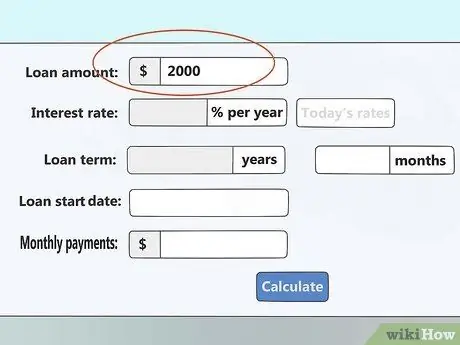
2. solis. Ievadiet aizdevuma summu
Šī ir kopējā aizņemtā naudas summa. Ja vēlaties aprēķināt daļēji samaksātu parādu, ievadiet atlikušo parādu, kas jums joprojām ir parādā.
Šīs slejas nosaukums varētu būt "pamatsumma"
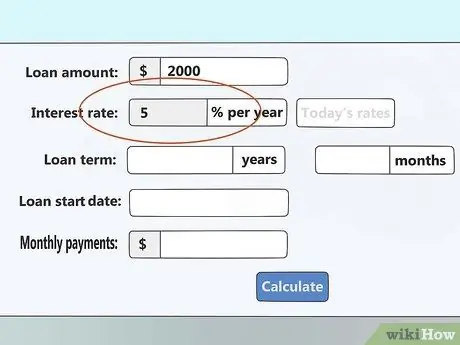
3. solis. Ievadiet procentu likmi
Šī ir pašreizējā procentu likme jūsu aizdevumam un ir procentos. Piemēram, ja jums jāmaksā 6% procentu likme, ierakstiet numuru
6. darbība
Palielinājuma intervālam šeit nav nozīmes. Noteiktajai procentu likmei jābūt gada procentu summai, pat ja šos procentus aprēķina biežāk

Solis 4. Ievadiet aizdevuma termiņu
Tas ir laiks, kuru plānojat dzēst parādu. Izmantojiet aizdevuma politikā norādīto laiku, lai aprēķinātu minimālo ikmēneša maksājumu, kas jāveic. Izmantojiet īsāku laiku, lai aprēķinātu lielākus maksājumus, lai varētu ātri nomaksāt parādus.
- Ātrāka parādu nomaksa nozīmē arī mazāk iztērētās naudas.
- Skatiet šo slejas šo tabulu, lai noteiktu, vai šis kalkulators izmanto mēneša vai gada sistēmu.

5. solis. Ievadiet sākuma datumu
To izmanto, lai aprēķinātu, kurā datumā jūs atmaksāsiet aizdevumu.
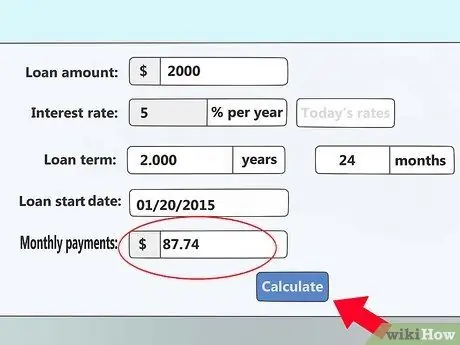
6. solis. Nospiediet aprēķināt (aprēķināt
) Daži kalkulatori automātiski atjauninās lauku "Ikmēneša maksājums" pēc informācijas ievadīšanas. Tomēr dažiem ir jāgaida, līdz jūs nospiežat pogu "aprēķināt", lai parādītu jūsu grafika grafiku.
- "Kredīta pamatsumma" ir sākotnējā parāda atlikusī summa, bet "procentu likme" ir aizdevuma papildu izmaksas.
- Šie kalkulatori parādīs informāciju par jūsu aizdevuma atmaksas grafiku pēc amortizētas principa (kredīts, kas tiek atmaksāts ar regulārām iemaksām), kas nozīmē, ka jūs katru mēnesi maksāsit to pašu summu.
- Ja maksājat mazāk par norādīto summu, aizdevuma termiņa beigās jums būs jāveic viens ļoti liels maksājums un jāmaksā lielāka summa.
2. metode no 3: aizdevuma maksājumu aprēķināšana manuāli
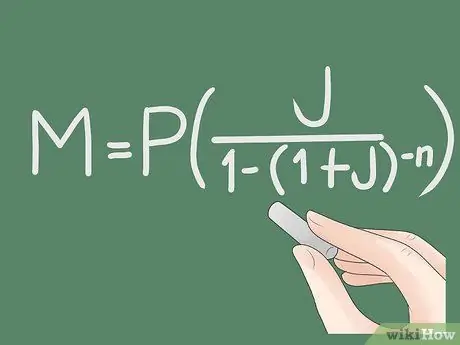
1. solis. Pierakstiet izmantoto formulu
Kredīta maksājumu aprēķināšanai izmantotā formula ir M = P * (J / (1 - (1 + J)-N)). Izpildiet šīs darbības, lai palīdzētu jums izmantot šo formulu, vai izpildiet īsu katra mainīgā skaidrojumu:
- M = maksājuma summa
- P = pamatsumma, kas nozīmē aizņemtās naudas summu
- J = efektīvā procentu likme. Paturiet prātā, ka tā parasti nav gada procentu likme, lūdzu, skatiet tālāk sniegto skaidrojumu.
- N = cik reizes jāmaksā

2. solis. Esiet uzmanīgi, noapaļojot rezultātus
Ideālā gadījumā izmantojiet grafisko kalkulatoru vai kalkulatora programmatūru, lai aprēķinātu visu formulu vienā rindā. Ja izmantojat kalkulatoru, ar kuru var veikt tikai pakāpeniskus aprēķinus, vai ja vēlaties veikt tālāk norādītās detalizētās darbības, pirms pāriet uz nākamo darbību, noapaļojiet līdz vismaz četriem nozīmīgiem skaitļiem. Noapaļojot līdz īsākai zīmei aiz komata, galīgajā atbildē var rasties būtiskas noapaļošanas kļūdas.
- Pat vienkāršiem kalkulatoriem parasti ir poga "Ans". Šī poga tiek izmantota, lai nākamajā aprēķinā ievadītu iepriekšējo atbildi, kuras rezultāts būs precīzāks nekā zemāk esošais aprēķins.
- Tālāk redzamie piemēri tiek aplūkoti pēc katra soļa, bet pēdējais solis ietver atbildi, ko saņemsiet, ja aprēķinu pabeigsiet vienā rindā, lai jūs varētu vēlreiz pārbaudīt savu darbu.
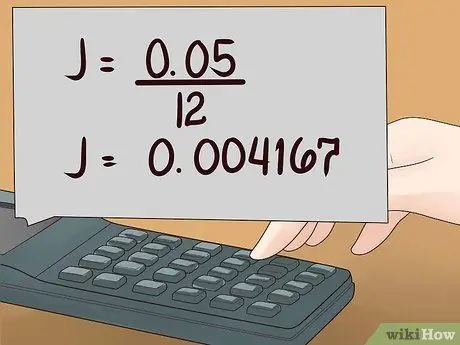
3. solis. Aprēķiniet savu efektīvo procentu likmi J
Aizdevuma politikā parasti ir norādīta "gada procentu likme", taču jūs nedrīkstat atmaksāt aizdevumu ikgadējās maksājumos. Sadaliet gada procentu likmi ar 100, lai iegūtu decimāldaļu, pēc tam daliet ar to, cik reizes katru gadu maksājat aizdevumu, lai iegūtu faktisko procentu likmi.
- Piemēram, ja jūsu gada procentu likme ir 5%un jūs maksājat ikmēneša maksājumos (12 reizes gadā), aprēķiniet 5/100, lai iegūtu 0,05, tad aprēķiniet J = 0,05 / 12 = 0, 004167.
- Neparastos gadījumos procentu likmes tiek aprēķinātas dažādos intervālos no maksājumu grafika. Galvenokārt hipotēkas Kanādā parasti tiek aprēķinātas divas reizes gadā, lai gan aizņēmēji maksājumus veic 12 reizes gadā. Šajā gadījumā gada procentu likme jāsadala ar diviem.

4. solis. Pievērsiet uzmanību kopējam maksājumu skaitam N
Jūsu aizdevuma politikā šis skaitlis jau var būt norādīts, vai arī jums tas būs jāaprēķina pašam. Piemēram, ja aizdevuma termiņš ir 5 gadi un jūs maksāsit ikmēneša maksājumos 12 reizes gadā, tad kopējais jūsu maksājumu skaits ir N = 5 * 12 = 60.
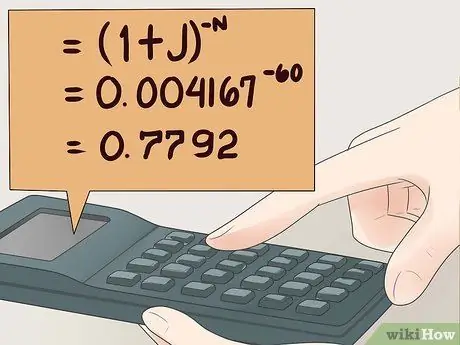
5. solis. Aprēķiniet (1+J)-N.
Vispirms pievienojiet 1+J, pēc tam palieliniet atbildi uz "-N" jaudu. Noteikti ievietojiet negatīvo zīmi zīmes N priekšā. Ja jūsu kalkulators nedarbojas ar negatīviem eksponentiem, varat uzrakstīt 1/((1+J)N).
Šajā piemērā (1+J)-N = (1.004167)-60 = 0, 7792

6. solis. Aprēķiniet J/(1- (jūsu atbilde))
Izmantojot vienkāršu kalkulatoru, vispirms aprēķiniet 1 - skaitli, kuru aprēķinājāt iepriekšējā solī. Pēc tam aprēķiniet J, dalītu ar rezultātu, iepriekšējā "J" aprēķinam izmantojot faktisko procentu likmi.
Šajā piemērā J/(1- (jūsu atbilde)) = 0, 004167/(1-0,7792) = 0, 01887

7. solis. Atrodiet ikmēneša maksājuma summu
Lai to aprēķinātu, reiziniet galīgo rezultātu ar aizdevuma summu P. Rezultāts ir naudas summa, kas jums jāmaksā katru mēnesi, lai savlaicīgi nomaksātu aizdevumu.
- Piemēram, ja jūs aizņēmāties 30 000 USD, jūs pēdējo atbildi reizinātu ar 30 000. Turpinot iepriekš minēto piemēru, 0,01887 * 30 000 = 566, 1 dolāru katru mēnesi jeb 566 USD un 10 centus.
- Tas attiecas uz visām valūtām, nevis tikai uz dolāriem.
- Ja visus šos piemērus aprēķināsit vienā rindā, izmantojot izdomātu kalkulatoru, jūs iegūsit precīzāku galveno izmaksu atbildi, rezultāts ir ļoti tuvu 566, 137 ASV dolāriem jeb aptuveni 566 ASV dolāriem un 14 centiem katru mēnesi. Ja mēs maksātu pat 566 USD un 10 centus katru mēnesi, kā mēs aprēķinājām, izmantojot iepriekš minēto mazāk precīzo kalkulatoru, aizdevuma termiņa beigās mēs būtu nedaudz mainījušies un, iespējams, būtu jāmaksā par dažiem dolāriem vairāk (šajā gadījumā mazāk par 5 USD) lieta.)
3. metode no 3: izpratne par aizdevumu darbību

1. solis. Izprotiet atšķirību starp aizdevumu ar fiksētu procentu likmi un aizdevumu ar regulējamu procentu likmi
Visos aizdevumos tiek izmantota viena no šīm divām kategorijām. Pārliecinieties, ka zināt, kāda veida aizdevums tiek piemērots:
- Kredīti ar fiksēti procenti ir fiksēta procentu likme. Jūsu ikmēneša maksājums nekad nemainīsies, ja vien samaksāsit savlaicīgi.
- Kredīti ar pielāgoti ziedi periodiski pielāgosies pašreizējai standarta procentu likmei, tāpēc, mainoties procentu likmēm, jums var būt lielāks vai mazāks parāds. Procentu likme tiek pārrēķināta tikai "pielāgošanās periodā", kas norādīts jūsu aizdevuma politikā. Ja jūs zināt, ka pašreizējā procentu likme ir tikai dažus mēnešus pirms nākamā pielāgošanās perioda, varat plānot uz priekšu.

2. solis. Izprotiet amortizāciju
Amortizācija attiecas uz likmi, ar kādu tiek samazināta sākotnējā aizņemtā summa (galvenais aizdevums). Kopumā ir divu veidu aizdevumu atmaksas grafiki:
- Kredīta maksājums ar pilnīga amortizācija aprēķināts tā, lai jūs varētu katru mēnesi samaksāt noteiktu summu visā atmaksas periodā, ar katru maksājumu nomaksājot pamatsummu un procentu likmes. Iepriekš minētie kalkulatori un formulas pieņem, ka vēlaties šādu grafiku.
- Kredīta atmaksas plāns ar vienkārši samaksājiet procentus nodrošina zemāku sākotnējo maksājumu "tikai procentu" periodā, jo jūs maksājat tikai procentus, nevis sākotnējo "pamatsummas" aizdevumu. Pēc procentu perioda beigām jūsu ikmēneša maksājumi būs milzīgi, jo jūs sāksit atmaksāt arī pamatsummu un procentus. Tas ilgtermiņā jums izmaksās vairāk naudas.

Solis 3. Maksājiet vairāk naudas iepriekš, lai ilgtermiņā ietaupītu vairāk naudas
Veicot papildu maksājumus, tiks samazināta naudas summa, kas jums jātērē ilgtermiņā, jo jo mazāka ir aizdevuma summa, uz kuru balstās procentu aprēķins. Jo ātrāk jūs to izdarīsit, jo vairāk naudas varēsiet ietaupīt.






