- Autors Jason Gerald [email protected].
- Public 2024-02-01 14:14.
- Pēdējoreiz modificēts 2025-01-23 12:26.
Pārvietošanās fizikā apzīmē objekta stāvokļa maiņu. Aprēķinot pārvietojumu, jūs aprēķināt, cik tālu objekts atrodas, pamatojoties uz tā sākotnējo un galīgo atrašanās vietu. Formula, ko izmanto, lai aprēķinātu pārvietojumu, ir atkarīga no problēmai dotā mainīgā. Lai aprēķinātu pārvietojumu, veiciet šīs darbības.
Solis
1. daļa no 5: Rezultātā iegūtā pārvietojuma aprēķināšana

1. solis. Izmantojiet iegūto pārvietojuma formulu, ja attāluma mērvienība tiek izmantota, lai norādītu sākuma un beigu vietu
Lai gan attālums atšķiras no pārvietojuma, no tā izrietošā pārvietošanas problēma meklē, cik kilometru vai metru objekts ir nobraucis. Jūs izmantosit šo mērvienību, lai aprēķinātu pārvietojumu un to, cik tālu objekta atrašanās vieta atšķiras no sākuma punkta.
- Rezultātā iegūtās pārvietošanas formula ir uzrakstīta šādi: S = x²+y². S ir pārvietojums. X ir objekta pirmais kustības virziens, bet Y - objekta otrais kustības virziens. Ja jūsu objekts pārvietojas tikai vienā virzienā, tad Y = 0.
- Objekts var pārvietoties ne vairāk kā divos virzienos, jo pārvietošanās pa ziemeļu/dienvidu vai austrumu/rietumu asi tiek uzskatīta par neitrālu kustību.

Solis 2. Savienojiet punktus kustības secībā un marķējiet tos no A līdz Z
Izmantojiet lineālu, lai no punkta uz punktu novilktu taisnu līniju.
- Atcerieties arī savienot sākuma punktu ar beigu punktu, izmantojot taisnu līniju. Tas ir pārvietojums, ko mēs aprēķināsim.
- Piemēram, ja objekts pārvietojas uz austrumiem 300 m un ziemeļiem 400 m, tas veidos taisnu trīsstūri. AB būs trijstūra pirmā kājiņa, bet BC būs otrā kājiņa. AC būs trīsstūra hipotenūza, un tā lielums ir objekta pārvietojums. Šajā piemērā abi virzieni ir austrumi un ziemeļi.

3. solis. Ievadiet x² un y² vērtības
Tagad, kad jūs zināt abus objekta kustības virzienus, ievadiet vērtības atbilstošajos mainīgajos.
Piemēram, x = 300 un y = 400. Jūsu formulai vajadzētu izskatīties šādi: S = 300² + 400²
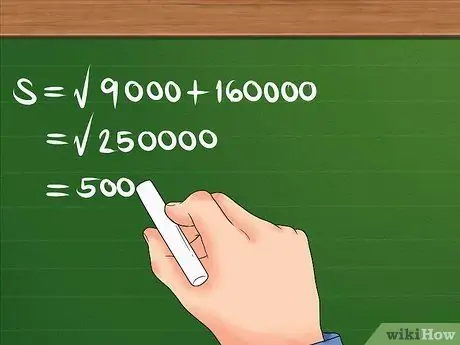
Solis 4. Aprēķiniet formulu, izmantojot darbību secību
Vispirms kvadrātus 300 un 400, pēc tam saskaitiet un atrodiet summas kvadrātsakni.
Piemēram: S = 90000 + 160000. S = 250000. S = 500. Tagad jūs zināt, ka pārvietojums ir 500 m
2. daļa no 5: Kad ir zināms ātrums un laiks

1. darbība. Izmantojiet šo formulu, ja problēma norāda objekta ātrumu un laiku, kas tam nepieciešams
Dažas matemātikas problēmas nepateiks, cik tālu vai cik ātri objekts pārvietojas. Jūs varat aprēķināt pārvietojumu, izmantojot šo laika un ātruma lielumu.
-
Šajā gadījumā formula kļūst šāda: S = 1/2 (u + v) t.
U = objekta sākotnējais ātrums vai cik ātri objekts sāk kustēties noteiktā virzienā. V = objekta galīgais ātrums vai tas, cik ātri objekts virzās uz savu galīgo atrašanās vietu. T = laiks, kas nepieciešams, lai objekts sasniegtu galīgo atrašanās vietu.
- Piemērs: automašīna nobrauc pa ceļu 45 sekundes (vajadzīgs laiks). Automašīna griežas uz rietumiem ar ātrumu 20 m/s (sākotnējais ātrums), un ceļa beigās tā ātrums ir 23 m/s (galīgais ātrums). Aprēķiniet pārvietojumu, pamatojoties uz šiem faktoriem.

2. solis Ievadiet vajadzīgo ātrumu un laiku atbilstošajos mainīgajos
Tagad, kad jūs zināt, cik tālu automašīna pārvietojas, cik ātri automašīna pārvietojas sākumā un beigās, varat atrast attālumu no sākuma vietas līdz galīgajai vietai.
Jūsu formulai vajadzētu izskatīties šādi: S = 1/2 (20 + 23) 45

Solis 3. Pēc vērtību ievietošanas pareizajā vietā aprēķiniet formulu
Atcerieties ievērot darbību secību, pretējā gadījumā pārvietojumu rezultātā tiks iegūtas ļoti atšķirīgas vērtības.
- Šai formulai nav nozīmes, ja nejauši maināt sākuma un beigu ātrumu. Tā kā šos skaitļus vispirms saskaitīsit kopā, nav nozīmes tam, kur tie ir iekavās. Tomēr citām formulām sākotnējā un beigu ātruma maiņa radīs atšķirīgas pārvietojuma vērtības.
- Jūsu formulai vajadzētu izskatīties šādi: S = 1/2 (43) 45. Vispirms sadaliet 43 ar 2, kā rezultātā iegūst 21, 5. Pēc tam reiziniet 21, 5 ar 45, tāpēc rezultāts ir 967,5 metri. 967, 5 ir jūsu pārvietojuma lielums vai tas, cik tālu automašīna ir pārvietojusies no sākuma punkta.
3. daļa no 5: Kad ir zināms sākotnējais ātrums, paātrinājums un laiks
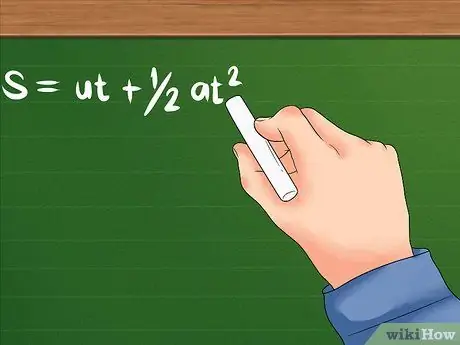
1. solis. Izmantojiet modificēto formulu, ja paātrinājums ir zināms papildus sākotnējam ātrumam un laikam
Daži jautājumi tikai pateiks, cik ātri objekts pārvietojas sākumā, cik ātri objekts sāk paātrināties un cik tālu objekts pārvietojas. Jums būs nepieciešama šāda formula.
- Šīs problēmas formula ir šāda: S = ut + 1/2at². U joprojām norāda sākotnējo ātrumu; a ir objekta paātrinājums vai cik ātri tā ātrums sāk mainīties. T var nozīmēt laiku, kas nepieciešams, vai noteiktu laiku, kas nepieciešams objekta paātrināšanai. Abi izmantos laika vienības, piemēram, sekundes, stundas un citas.
- Pieņemsim, ka automašīna, kas pārvietojas ar ātrumu 25 m/s (sākotnējais ātrums), sāk paātrināties ar ātrumu 3 m/s2 (paātrinājums) 4 sekundes (laiks). Kāds ir automašīnas pārvietojums pēc 4 sekundēm?

2. solis. Ievadiet vērtības formulā
Atšķirībā no iepriekšējās formulas šeit ir attēlots tikai sākotnējais ātrums, tāpēc noteikti ievadiet pareizos datus.
Pamatojoties uz iepriekš minētajiem parauga datiem, jūsu formula izskatītos šādi: S = 25 (4) + 1/2 (3) 4². Tas palīdz pievienot iekavas ap jūsu paātrinājuma lielumu un laiku, lai palīdzētu atdalīt skaitļus
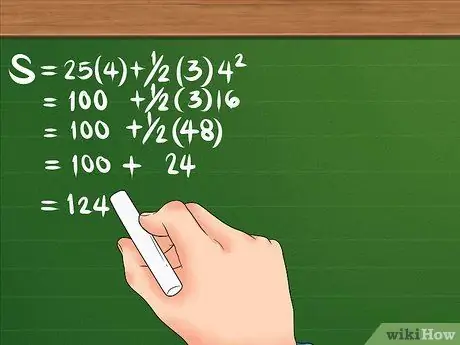
3. solis. Aprēķiniet pārvietojumu, veicot to pareizā darbību secībā
Ātrs veids, kā palīdzēt atcerēties darbību secību, ir ēzeļa tilts Kur ir Kua ci Kadang Ba wa Juragan Turtles. Tas attēlo pareizo secību: iekavas, kvadrātus, reizināšanu, dalīšanu, saskaitīšanu un atņemšanu.
Apskatīsim formulu vēlreiz: S = 25 (4) + 1/2 (3) 4². Pirmkārt, kvadrāts 4, rezultāts ir 16. Tad reiziniet 16 ar 3, padarot 48; tad arī reiziniet 25 ar 4, lai iegūtu 100. Sadaliet 48 ar 2, lai iegūtu 24. Jūsu vienādojumam vajadzētu izskatīties šādi: S = 100 + 24. Kad esat saskaitījis abus kopā, pārvietojums ir 124 metri
4. daļa no 5: leņķiskā pārvietojuma aprēķināšana

1. solis. Atrodiet leņķisko pārvietojumu, kad objekts pārvietojas apļveida ceļā
Lai gan jūs joprojām aprēķināsiet pārvietojumu, izmantojot taisnu līniju, jums jāatrod atšķirība starp objekta sākuma un beigu atrašanās vietu, kad tas pārvietojas apļveida ceļā.
- Iedomājieties meiteni, kas sēž karuselī. Griežoties ar karuseli, viņš pārvietosies pa apļveida ceļu. Leņķiskais pārvietojums mēģina atrast īsāko attālumu starp sākotnējo un beigu vietu, kad objekts nepārvietojas taisnā līnijā.
- Leņķa pārvietošanas formula ir šāda: = S/r, kur S ir lineārais pārvietojums, r ir rādiuss un ir leņķiskais pārvietojums. Lineāra pārvietošana ir objekta pārvietošanās attālums pa loka līniju. Rādiuss ir objekta attālums līdz apļa centram. Leņķiskais pārvietojums ir vērtība, kuru mēs vēlamies atrast.

Solis 2. Pievienojiet vienādojumam lineāro pārvietojumu un rādiusu
Atcerieties, ka rādiuss ir attālums no apļa centra; dažas problēmas jums pateiks apļa diametru, kas jāsadala ar 2, lai atrastu rādiusu.
- Šeit ir problēmas piemērs: meitene brauc karuselī. Sēdeklis atrodas 1 metra attālumā no apļa centra (rādiuss). Ja meitene pārvietojas loka trajektorijā 1,5 metrus (lineāra nobīde), kāds ir viņas leņķiskais pārvietojums?
- Jūsu vienādojums izskatīsies šādi: = 1,5/1.
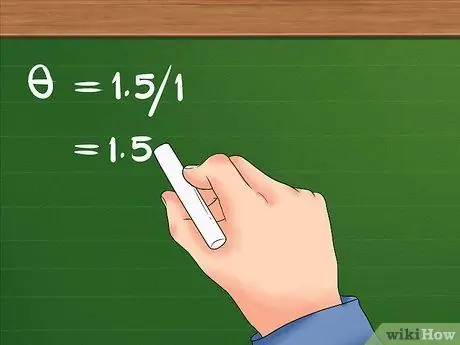
Solis 3. Sadaliet lineāro pārvietojumu ar rādiusu
Šis sadalījums novedīs pie objekta leņķiskā pārvietojuma.
- Pēc 1,5 dalīšanas ar 1 rezultāts ir 1,5. Meitenes leņķiskais pārvietojums ir 1,5 radiāni.
- Tā kā leņķiskais pārvietojums mēra, cik daudz objekts griežas no sākotnējās pozīcijas, tas jāmēra kā leņķis, nevis attālums. Radiāns ir mērvienība, ko izmanto leņķu mērīšanai.
5. daļa no 5: Izpratne par migrāciju
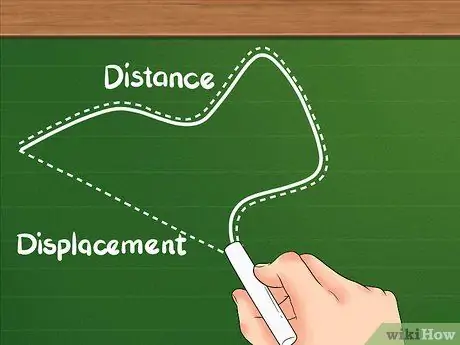
1. solis. Ziniet, ka attālumam ir atšķirīga definīcija nekā pārvietojumam
Attālums parāda, cik tālu kopējais objekta nobrauktais attālums.
- Attālumu bieži sauc par skalāru daudzumu. Attālums parāda objekta nobraukto attālumu neatkarīgi no objekta virziena.
- Piemēram, ja jūs ejat 2 soļus uz austrumiem, 2 soļus uz dienvidiem, 2 soļus uz rietumiem un pēc tam 2 soļus uz ziemeļiem, jūs atgriezīsities sākuma stāvoklī. Pat ja jūs esat izgājis cauri kopējam attālums Tikai 10 soļu attālumā pārvietot 0 soļu attālumā, jo jūsu galīgā atrašanās vieta ir tāda pati kā sākuma vieta (jūsu ceļš atgādina lodziņu).

2. solis. Saprotiet, ka pārvietojums ir atšķirība starp divām vietām
Pārvietojums nav kopējā kustību summa, piemēram, attālums; pārmaiņas koncentrējas uz apgabalu starp sākuma un beigu vietu.
- Pārvietojumu sauc par vektora lielumu, un tas parāda objekta stāvokļa izmaiņas, ņemot vērā objekta kustības virzienu.
- Piemēram, jūs ejat uz austrumiem piecus soļus. Ja atgriežaties 5 rietumu virzienā uz rietumiem, pārvietojaties pretējā virzienā no sākotnējās atrašanās vietas. Pat ja esat veicis 10 soļus, jūsu pozīcija nav mainījusies; jūsu pārvietojums ir 0 soļi.

3. solis. Mēģinot iedomāties pārvietošanos, atcerieties vārdus uz priekšu un atpakaļ
Pārvietošanās pretējā virzienā novērš objekta pārvietošanos.
Iedomājieties futbola treneri turp un atpakaļ malā. Kliedzot uz spēlētājiem, viņš vairākas reizes pārslēdzās no kreisās uz labo pusi. Ja vērojat viņu, kad viņš pārvietojas no kreisās uz labo pusi, jūs novērojat kopējo nobraukto attālumu. Tomēr pieņemsim, ka treneris apstājas, lai sarunātos ar aizsargu malā. Ja viņš pirms pārvietošanās atrodas citā vietā nekā sākotnējā atrašanās vieta, tad jūs novērojat trenera kustību

4. solis. Ziniet, ka pārvietojumu mēra, izmantojot taisnu, nevis apļveida ceļu
Lai atrastu pārvietojumu, jums jāatrod īsākais un efektīvākais veids, kā aprēķināt starpību starp diviem punktiem.
- Apļveida ceļš jūs aizvedīs no sākuma vietas līdz galamērķim, taču tas nav īsākais ceļš. Lai palīdzētu jums to vizualizēt, iedomājieties, ka ejat taisnā līnijā un saskaraties ar stabu. Jūs nevarat izlauzties cauri šim pīlāram, tāpēc apejat to. Lai gan jūsu galīgā pozīcija ir tāda pati kā tad, ja jūs izlauzāt pīlāru, šī mērķa sasniegšanai jums būs jāveic papildu darbības.
- Lai gan pārvietojums ir taisns ceļš, ziniet, ka varat izmērīt objekta pārvietojumu pašlaik pārvietoties apļveida ceļā. Šo pārvietojumu sauc par leņķisko pārvietojumu, un to var aprēķināt, atrodot īsāko ceļu no sākotnējās atrašanās vietas līdz galīgajai atrašanās vietai.

5. solis. Ziniet, ka pārvietošanās var būt negatīva, atšķirībā no attāluma
Ja jūsu galīgā atrašanās vieta tiek sasniegta, pārvietojoties pretējā virzienā jūsu sākotnējam virzienam, tad pārvietojums ir negatīvs.
- Piemēram, mēs ejam 5 soļus uz austrumiem un pēc tam 3 soļus uz rietumiem. Pat ja pēc aprēķina jūs pārvietojat 2 soļus no sākuma vietas, jūsu pārvietojums ir -2, jo pārvietojaties pretējā virzienā. Jūsu attālums vienmēr būs pozitīvs, jo jūs nevarat skaitīt atpakaļ soļos, kilometros utt.
- Negatīvs pārvietojums nenozīmē, ka pārvietojums samazinās. Negatīvs nozīmē tikai to, ka virziens ir pretējs.

6. Apzinieties, ka dažreiz attālums un pārvietojums var būt vienādi
Ja staigājat taisni 25 soļus un apstājaties, nobrauktais attālums būs vienāds ar pārvietojumu no sākotnējās atrašanās vietas.
- Tas attiecas tikai tad, ja pārvietojaties no vienas vietas no sākuma vietas taisnā līnijā. Piemēram, jūs dzīvojat Sanfrancisko, Kalifornijā, un iegūstat jaunu darbu Lasvegasā, Nevadas štatā. Jums ir jāpārceļas uz Lasvegasu, lai būtu tuvu savam darbam. Ja iekāpjat lidmašīnā, kas lido taisni no Sanfrancisko līdz Lasvegasai jūs nobrauksit tādu pašu attālumu un pārvietojumu x.
- Tomēr, ja braucat no Sanfrancisko uz Lasvegasu, jūs nobrauksit attālumu x, bet nobrauksiet y. Tā kā braukšanai ar automašīnu parasti ir dažādi virzieni (uz austrumiem no šī ceļa, uz rietumiem no šī ceļa), jūs nobrauksit lielākus attālumus nekā īsākais attālums starp abām pilsētām.






