- Autors Jason Gerald [email protected].
- Public 2023-12-16 11:26.
- Pēdējoreiz modificēts 2025-01-23 12:26.
Frakciju pievienošana ir ļoti noderīga zināšana. Šo prasmi ir ļoti viegli iemācīties un izmantot, strādājot pie matemātikas problēmām no pamatskolas līdz vidusskolai. Šajā rakstā ir paskaidrots, kā pievienot frakcijas, lai to paveiktu tikai dažu minūšu laikā.
Solis
1. metode no 2: Frakciju pievienošana ar vienu un to pašu saucēju

1. solis. Pārbaudiet katras frakcijas saucēju (skaitli zem koeficienta)
Ja skaitļi ir vienādi, jūs pievienojat frakcijas ar vienu un to pašu saucēju. Ja saucēji ir atšķirīgi, izlasiet otro metodi.
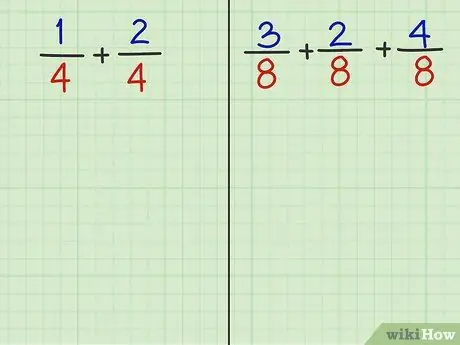
2. solis. Atbildiet uz šādiem 2 jautājumiem
Izlasot šīs metodes pēdējo soli, jums vajadzētu būt iespējai saskaitīt nākamo divu jautājumu daļas.
- 1. problēma: 1/4 + 2/4
- 2. problēma: 3/8 + 2/8 + 4/8
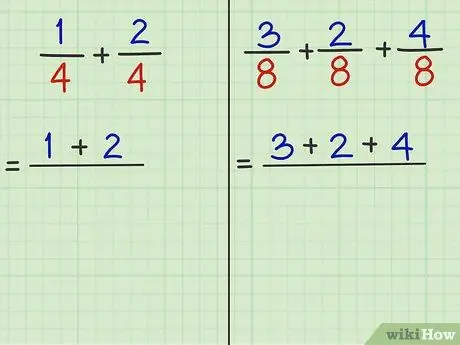
Solis 3. Savāc skaitītājus (ciparus virs dalījuma) un sasummē tos
Skaitītājs ir skaitlis virs koeficienta. Neatkarīgi no tā, cik daudz frakciju vēlaties pievienot, skaitītājus varat pievienot uzreiz, ja saucēji ir vienādi.
- 1. problēma: 1/4 + 2/4 ir pievienojamā daļa. "1" un "2" ir skaitītāji. Tātad, 1 + 2 = 3.
- 2. problēma: 3/8 + 2/8 + 4/8 ir pievienojamā daļa. "3" un "2" un "4" ir skaitītāji. Tātad, 3 + 2 + 4 = 9.

4. solis. Nosakiet jauno daļu no summas
Pierakstiet 2. solī iegūto skaitītāju. Šis skaitlis ir jauns skaitītājs. Uzrakstiet saucēju, kas ir vienāds skaitlis zem katras frakcijas dalītāja. Jums nav jāveic aprēķini, ja saucēji ir vienādi. Šis skaitlis ir jauns saucējs un vienmēr ir vienāds ar veco saucēju, pievienojot frakcijas ar vienu un to pašu saucēju.
- 1. problēma: 3 ir jaunais skaitītājs un 4 ir jaunais saucējs. Tādējādi atbilde uz pirmo jautājumu ir 3/4. 1/4 + 2/4 = 3/4.
- 2. problēma: 9 ir jaunais skaitītājs un 8 ir jaunais saucējs. Tādējādi atbilde uz otro jautājumu ir 9/8. 3/8 + 2/8 + 4/8 = 9/8.
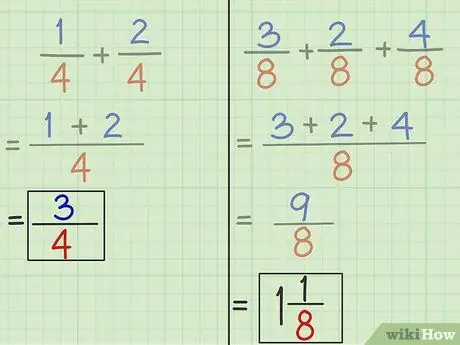
5. solis. Ja nepieciešams, vienkāršojiet frakcijas
Neaizmirstiet vienkāršot jauno frakciju, lai padarītu rakstīšanu vienkāršāku.
-
Ja skaitītājs lielāks saucēja vietā, piemēram, 2. uzdevuma pievienošanas rezultāts, tas nozīmē, ka mēs iegūstam veselu mēnesi pēc frakcijas vienkāršošanas. Sadaliet skaitītāju ar saucēju vai 9 dalot ar 8. Rezultāts ir vesels skaitlis 1, kas paliek 1. Rakstiet veseli skaitļi daļas priekšā, bet pārējais kļūst par skaitļa skaitītāju ar tādu pašu saucēju.
9/8 = 1 1/8.
2. metode no 2: Frakciju pievienošana ar dažādiem saucējiem

1. solis. Pārbaudiet katras frakcijas saucēju (skaitli zem koeficienta)
Ja saucēji ir atšķirīgi, jūs esat pievienojiet frakcijas ar dažādiem saucējiem. Izlasiet tālāk norādītās darbības, jo pirms frakciju pievienošanas saucējiem ir jābūt vienādiem.
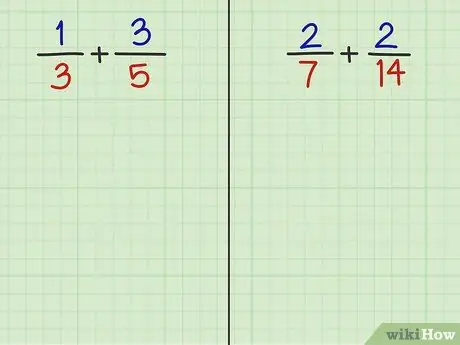
2. solis. Atrisiniet šādus 2 jautājumus
Izlasot šīs metodes pēdējo soli, jums vajadzētu būt iespējai saskaitīt nākamo divu jautājumu daļas.
- 3. problēma: 1/3 + 3/5
- 4. jautājums: 2/7 + 2/14

Solis 3. Saskaņojiet saucējus
Lai to izdarītu, reiziniet divu iepriekš minēto frakciju saucējus. Vienkāršs veids, kā izlīdzināt saucējus, ir reizināt abu frakciju saucējus. Ja viens no saucējiem ir otra reizinājums, atrodiet vismazāko kopīgo no diviem saucējiem.
-
3. problēma:
3 x 5 = 15. Tātad abu frakciju jaunais saucējs ir 15.
-
4. problēma:
14 ir 7. reizinājums. Tāpēc mums tikai jāreizina 7 ar 2, lai iegūtu 14. Tādējādi abu frakciju jaunais saucējs ir 14.

4. solis. Reiziniet pirmās frakcijas skaitītāju un saucēju ar otrās frakcijas saucēju
Šis solis nemaina frakcijas vērtību, bet šķiet, ka daļa mainās, lai tā atbilstu saucējam. Sadalījuma vērtība paliek nemainīga.
-
3. problēma:
1/3 x 5/5 = 5/15.
-
4. problēma:
Lai atrisinātu šo problēmu, mums vienkārši jāreizina pirmā daļa ar 2/2, lai saucēji būtu vienādi.
2/7 x 2/2 = 4/14

Solis 5. Reiziniet otrās frakcijas skaitītāju un saucēju ar pirmās frakcijas saucēju
Līdzīgi kā iepriekš minētās darbības, mēs nemainām frakcijas vērtību, bet šķiet, ka daļa mainās, lai izlīdzinātu saucēju. Sadalījuma vērtība paliek nemainīga.
-
3. problēma:
3/5 x 3/3 = 9/15.
-
4. problēma:
Mums nav jāreizina otrā daļa, jo saucēji ir vienādi.

6. solis. Uzrakstiet divas jaunās frakcijas secībā
Šobrīd mēs neesam saskaitījuši abas frakcijas kopā, lai gan varam. Iepriekšējā solī mēs katru frakciju reizinājām ar 1. Tagad mēs vēlamies pārliecināties, vai pievienotajām daļām ir vienāds saucējs.
-
3. problēma:
1/3 + 3/5 vietā daļa kļūst par 5/15 + 9/15
-
4. problēma:
2/7 + 2/14 vietā daļa kļūst par 4/14 + 2/14

7. solis. Pievienojiet abu frakciju skaitītājus kopā
Skaitītājs ir skaitlis virs koeficienta.
-
3. problēma:
5 + 9 = 14. 14 ir jaunais skaitītājs.
-
4. problēma:
4 + 2 = 6. 6 ir jaunais skaitītājs.

8. solis. Uzrakstiet kopsaucēju (2. solī) zem jaunā skaitītāja vai izmantojiet daļas saucēju, kas reizināts ar 1, lai izlīdzinātu saucēju
-
3. problēma:
15 ir jaunais saucējs.
-
4. problēma:
14 ir jaunais saucējs.

9. solis. Uzrakstiet jaunu skaitītāju un jaunu saucēju
-
3. problēma:
14/15 ir atbilde 1/3 + 3/5 =?
-
4. problēma:
6/14 ir atbilde 2/7 + 2/14 =?

10. solis. Vienkāršojiet un samaziniet frakcijas
Lai vienkāršotu frakcijas, daliet skaitītāju un saucēju ar lielāko kopējo koeficientu no diviem skaitļiem.
-
3. problēma:
14/15 nevar vienkāršot.
-
4. problēma:
6/14 var samazināt līdz 3/7 pēc skaitītāja un saucēja dalīšanas ar 2 kā lielāko kopējo koeficientu 6 un 14.
Padomi
- Pirms frakciju pievienošanas pārliecinieties, ka saucēji ir vienādi.
- Nesummējiet saucējus. Ja saucēji ir vienādi, pēc frakciju pievienošanas izmantojiet skaitli kā saucēju.
- Ja vēlaties pievienot frakcijas ar skaitļiem, kas sastāv no veseliem skaitļiem un daļām, konvertējiet šos skaitļus par daļām un saskaitiet tos saskaņā ar iepriekš sniegtajiem norādījumiem.






