Krusteniskā reizināšana ir veids, kā atrisināt vienādojumus, kas ietver divu ekvivalentu frakciju mainīgo. Mainīgais ir vietturis nezināmam skaitļu daudzumam, un krustota reizināšana pārvērš to par vienkāršu vienādojumu, ļaujot jums atrast attiecīgā mainīgā vērtību. Krustveida reizināšana ir ļoti noderīga, ja vēlaties pabeigt salīdzinājumu. Lūk, kā to izdarīt:
Solis
1. metode no 2: viena mainīgā krustojums
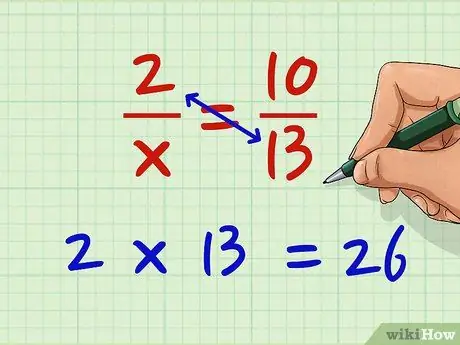
1. solis. Reiziniet kreisās daļas skaitītāju ar labās frakcijas saucēju
Pieņemsim, ka vēlaties atrisināt vienādojumu 2/x = 10/13. Tagad reiziniet 2 ar 13,2 x 13 = 26.
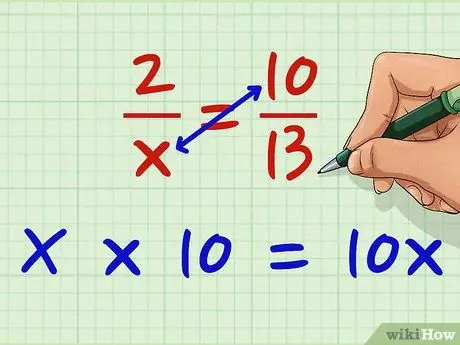
2. solis. Reiziniet labās puses saucēju ar kreiso saucēju
Reiziniet x ar 10. X * 10 = 10x. Vispirms varat šķērsot šo sadaļu; tam nav nozīmes, ja jūs abus skaitītājus reizina ar abiem saucējiem pa diagonāli.
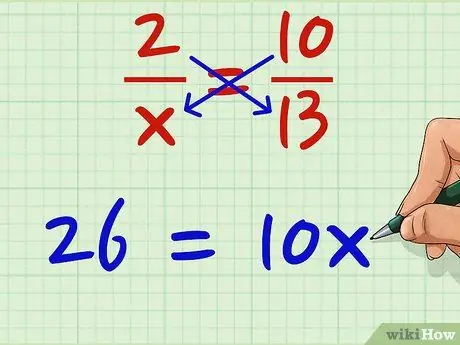
Solis 3. Padariet abus produktus vienādus
26 ir vienāds ar 10x. 26 = 10 reizes. Nav svarīgi, kurš no tiem atrodas labajā vai kreisajā pusē; būdami vienādi, varat mainīt viņu atrašanās vietu, ja vien pārvietojat tos visus uzreiz.
Tātad, ja jūs mēģināt atrast x vērtību 2/x = 10/13, 2 * 13 = x * 10 vai 26 = 10x
Solis 4. Atrodiet mainīgā vērtību
Tagad, kad jums ir 26 = 10x, varat mēģināt atrast kopīgu skaitītāju un dalīt 26 un 10 ar to pašu skaitli, kas dala abus. Tā kā abi ir pāra skaitļi, varat dalīt ar 2; 26/2 = 13 un 10/2 = 5. Pārējais ir 13 = 5x. Tagad, ņemot vien x, sadaliet abas vienādojuma puses ar 5. Tātad 13/5 = 5/5 vai 13/5 = x. Ja vēlaties atbildi decimāldaļā, varat sākt, dalot abas vienādojuma puses ar 10, lai iegūtu 26/10 = 10/10 vai 2,6 = x.
2. metode no 2: daudzfaktoru krusteniskā reizināšana
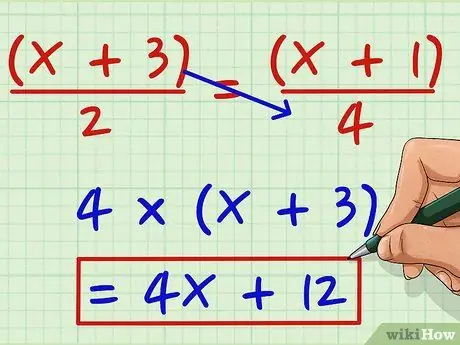
Solis 1. Reiziniet skaitītāju pa kreisi ar saucēju labajā pusē
Pieņemsim, ka vēlaties atrisināt šādu vienādojumu: (x + 3)/2 = (x + 1)/4. Reiziniet (x + 3) ar 4, lai iegūtu 4 (x + 3). Reiziniet ar 4, lai iegūtu 4x + 12.
Solis 2. Reiziniet skaitītāju labajā pusē ar saucēju pa kreisi
Atkārtojiet procesu otrā pusē. (x+1) x 2 = 2 (x+1). Reiziniet ar 2, lai iegūtu 2x + 2.
Solis 3. Padariet abu produktu reizinājumu un apvienojiet tos pašus mainīgos
Tagad rezultāts ir 4x + 12 = 2x + 2. Apvienojiet mainīgo x un konstanti vienādojuma otrā pusē.
- Tātad, apvienojiet 4x un 2x, atņemot 2x no abām pusēm. Atņemot 2x no 2x, atlikums būs 0. Kreisajā pusē 4x - 2x = 2x, tātad atlikums ir 2x.
- Tagad apvienojiet 12 un 2, atņemot 12 no abām pusēm. Atņemiet 12 no 12 kreisajā pusē un rezultāts ir 0, tad atņemiet 12 no 2 labajā pusē, lai rezultāts būtu 2 -12 = -10.
- Pārējais ir 2x = -10.
Solis 4. Pabeigt
Viss, kas jums jādara, ir sadalīt abas vienādojuma puses ar 2. 2x/2 = -10/2 = x = -5. Pēc krusteniskās reizināšanas jūs atradīsit, ka x = -5. Jūs varat atgriezties un pārbaudīt savu darbu, ievadot x vērtību, kas ir -5, lai pārliecinātos, ka abas puses ir vienādas. Tas izrādījās līdzvērtīgs. Ja pievienojat sākotnējo vienādojumu -5, rezultāts ir -1 = -1.
Padomi
- Ņemiet vērā: ja vienā un tajā pašā vienādojumā pievienojat dažādus skaitļus (piemēram, 5), rezultāts ir 2/5 = 10/13. Pat ja jūs reizināt kreiso pusi ar vēl 5/5, jūs saņemat 10/25 = 10/13, kas ir acīmredzami nepareizi. Šis gadījums norāda, ka esat pieļāvis krustojuma reizināšanas kļūdu.
- Jūs varat pārbaudīt savu atbildi, pievienojot rezultātu sākotnējam vienādojumam. Ja vienādojums ir patiess apgalvojums, piemēram, 1 = 1, jūsu atbilde ir pareiza. Ja vienādojums kļūst par nepatiesu apgalvojumu, piemēram, 0 = 1, jūs pieļāvāt kļūdu. Piemēram, pievienojiet 2, 6 vienādojumam tā, lai 2/(2, 6) = 10/13. Reiziniet kreiso pusi ar 5/5, lai iegūtu 10/13 = 10/13. Rezultāts ir pareizs apgalvojums, kas vienkāršots kļūst par 1 = 1, tātad 2, 6 ir pareizā atbilde.
