- Autors Jason Gerald [email protected].
- Public 2023-12-16 11:26.
- Pēdējoreiz modificēts 2025-01-23 12:27.
Skaitļa kvadrātsakni ir viegli atrast, ja atbilde ir vesels skaitlis. Ja atbilde nav vesels skaitlis, ir virkne procesu, kuriem varat sekot, lai iegūtu kvadrātsakni, pat ja neizmantojat kalkulatoru. Lai to izdarītu, jums ir jāsaprot reizināšanas, saskaitīšanas un dalīšanas pamati.
Solis
1. metode no 3: vesela skaitļa kvadrātsaknes atrašana
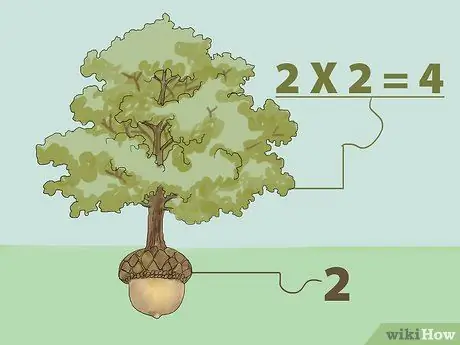
1. solis. Atrodiet perfektu kvadrātsakni, reizinot
Skaitļa kvadrātsakne ir skaitlis, kuru reizinot ar sevi, tiek atgriezts sākotnējais skaitlis. Citiem vārdiem sakot: "Kādu skaitli mēs varam reizināt ar sevi, lai iegūtu vēlamo skaitli?"
- Piemēram, kvadrātsakne no 1 ir 1, jo 1, kas reizināts ar 1, ir 1 (1X1 = 1). Tādējādi kvadrātsakne no 4 ir 2, jo 2, kas reizināts ar 2, ir 4 (2X2 = 4). Iedomājieties kvadrātsaknes koncepciju kā koku. Koks aug no sēklām. Tātad koks ir lielāks par sēklu, kas aug no sēklas, kas ir tā sakne. No iepriekš minētā piemēra 4 ir koks, un 2 ir sēkla.
- Tātad kvadrātsakne no 9 ir 3 (3X3 = 9), no 16 ir 4 (4X4 = 16), no 25 ir 5 (5X5 = 25), no 36 ir 6 (6X6 = 36), no 49 ir 7 (7X7 = 49), no 64 ir 8 (8X8 = 64), no 81 ir 9 (9X9 = 81) un no 100 ir 10 (10X10 = 100).
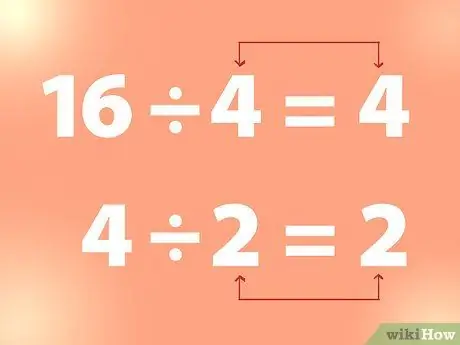
2. solis. Izmantojiet nepārtrauktu dalīšanu, lai atrastu kvadrātsakni
Lai atrastu vesela skaitļa kvadrātsakni, varat to sadalīt ar skaitli, līdz iegūstat skaitli, kas ir vienāds ar dalītāju.
- Piemērs: 16 dalīts ar 4 ir 4. Un 4 dalīts ar 2 ir 2 utt. Tādējādi no iepriekš minētā piemēra 4 ir kvadrātsakne no 16 un 2 ir kvadrātsakne no 4.
- Perfektām kvadrātsaknēm nav frakciju vai decimāldaļu, jo tās ir veseli skaitļi.
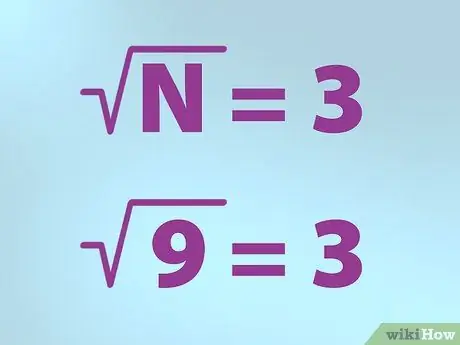
3. Izmantojiet pareizo kvadrātsaknes simbolu
Matemātiķi izmanto īpašu simbolu, lai attēlotu kvadrātsakni. Forma ir kā atzīme ar plus līniju augšējā labajā stūrī.
- N ir vienāds ar skaitli, kuram vēlaties atrast kvadrātsakni. N ir ievietots zem atzīmes.
- Tātad, ja vēlaties atrast kvadrātsakni no 9, uzrakstiet formulu, ieliekot atzīmi "N" (9) atzīmes iekšpusē (simbols "sakne"), pēc tam ierakstiet vienādības zīmi un pēc tam 3. Tas nozīmē "kvadrātsakne no 9 ir vienāds ar 3 ".
2. metode no 3: cita skaitļa kvadrātsaknes atrašana
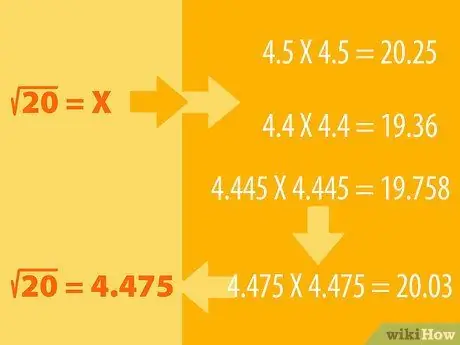
Solis 1. Uzminiet un veiciet likvidēšanas procesu
Ir grūti atrast skaitļa, kas nav vesels skaitlis, kvadrātsakni. Tomēr tas nenozīmē, ka tas nav iespējams.
- Piemēram, pieņemsim, ka vēlaties atrast kvadrātsakni no 20. Mēs zinām, ka 16 ir ideāls kvadrāts, kura kvadrātsakne ir 4 (4X4 = 16). Tad 25 kvadrātsaknes ir 5 (5X5 = 25), tāpēc kvadrātsaknei no 20 jāatrodas starp abām.
- Jūs varat uzminēt, ka kvadrātsakne no 20 ir 4,5. Tagad kvadrāts 4,5, lai redzētu rezultātu. Tas ir, mēs reizinām 4, 5 ar sevi: 4, 5X4, 5. Skatiet, vai atbilde ir lielāka vai mazāka par 20. Ja jūsu minējums ir pārāk tālu, izmēģiniet citu skaitli (piemēram, 4, 6 vai 4, 4) un pielāgojiet uzminiet, līdz jūs iegūstat skaitli 20.
- Piemēram, 4, 5X4, 5 = 20, 25, tāpēc loģiski, ka mums jāatrod mazāks skaitlis, iespējams, 4, 4. 4, 4X4, 4 = 19, 36. Tātad kvadrātsaknei no 20 jābūt starp 4, 5 un 4, 4. Izmēģiniet ar 4, 445X4, 445. Rezultāts ir 19, 758. Rezultāts tuvojas. Turpiniet mēģināt izmantot citus skaitļus, līdz iegūstat 4, 475X4, 475 = 20, 03. Noapaļojot, šis skaitlis ir vienāds ar 20.

2. solis. Izmantojiet vidējās vērtības noteikšanas procesu
Šis process arī sākas, atrodot divus tuvākos perfektos kvadrātus, kuriem blakus ir skaitlis.
- Tad sadaliet šo skaitli ar vienu no perfektajām kvadrātsaknēm. Ņemiet atbildi, pēc tam atrodiet vidējo vērtību starp šo skaitli un skaitli, kura sakni vēlaties atrast (vidējo var atrast, saskaitot abus kopā un dalot ar diviem). Pēc tam daliet sākotnējo skaitli ar iegūto vidējo. Pēdējais solis, atrodiet rezultātu vidējo ar pirmo reizi aprēķināto vidējo.
- Izklausās sarežģīti? Būtu vieglāk, ja sniegtu piemēru. Piemēram, 10 atrodas starp diviem perfektiem kvadrātiem 9 (3X3 = 9) un 16 (4X4 = 16). Abu skaitļu kvadrātsaknes ir 3 un 4. Tātad, daliet 10 ar pirmo skaitli 3. Rezultāts ir 3, 33. Tagad atrodiet vidējo 3 un 3, 33, saskaitot tos un dalot ar 2. Rezultāts ir 3, 1667 Tagad daliet 10 ar 3,1667. Rezultāts ir 3.1579. Tad atrodiet vidējo vērtību 3.1579 un 3.1667, saskaitot tos un dalot ar 2. Rezultāts ir 3.1623.
- Pārbaudiet rezultātu, reizinot atbildi (šajā 3, 1623. piemērā) ar sevi. Rezultāts 3.1623, kas reizināts ar 3.1623, izrādās 10.001.
3. metode no 3: negatīvo skaitļu kvadrācija
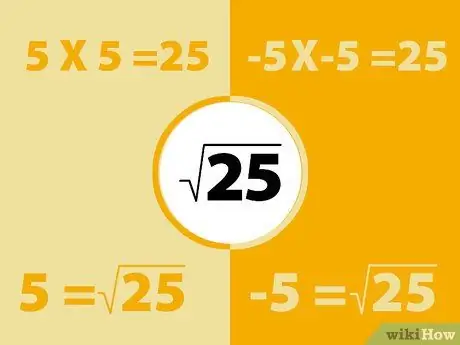
Solis 1. Kvadrējiet negatīvos skaitļus, izmantojot to pašu metodi
Atcerieties, ka negatīvs negatīvs laiks ir pozitīvs. Tātad negatīva skaitļa kvadrāts radīs pozitīvu skaitli.
- Piemēram, -5X -5 = 25. Tomēr atcerieties arī to, ka 5x5 = 25. Tātad kvadrātsakne no 25 var būt -5 vai 5. Būtībā katram skaitlim ir divas kvadrātsaknes.
- Līdzīgi 3X3 = 9 un -3X -3 = 9, tāpēc kvadrātsaknes no 9 ir 3 un -3. Pozitīvo kvadrātsakni sauc par "galveno sakni". Šajā brīdī mums vienkārši jāpievērš uzmanība šai atbildei.
2. solis. Izmantojiet kalkulatoru
Lai gan matemātiku vislabāk var veikt ar rokām, kvadrātveida sakņu aprēķināšanai ir pieejami daudzi tiešsaistes kalkulatori.
- Parastā kalkulatorā meklējiet kvadrātsaknes pogu.
- Tiešsaistes kalkulatorā tieši ievadiet numuru, kuram vēlaties atrast kvadrātsaknes vērtību, un noklikšķiniet uz pogas. Dators parādīs kvadrātsaknes vērtību.
Padomi
-
Vienmēr paturiet prātā dažus svarīgus perfektus kvadrātus:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Atcerieties arī šo perfekto kvadrātu: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Ņemiet vērā arī šo: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






