- Autors Jason Gerald [email protected].
- Public 2023-12-16 11:26.
- Pēdējoreiz modificēts 2025-01-23 12:27.
Decimāldaļu (bāzes desmit) skaitļu sistēmai ir desmit iespējamās vērtības (0, 1, 2, 3, 4, 5, 6, 7, 8 vai 9) katrai skaitļa pozīcijai. Turpretī binārajai (otrās bāzes) skaitļu sistēmai ir tikai divas iespējamās vērtības, kuras katrai skaitļa pozīcijai attēlo ar 0 un 1. Tā kā bināro skaitļu sistēma ir elektronisko datoru iekšējā valoda, nopietni datoru programmētāji zina, kā pārvērst no decimālā uz bināro skaitļu sistēmu. Izpildiet šīs vienkāršās darbības un arī to, kā apgūt šo reklāmguvumu.
Solis
1. metode no 2: īsa dalīšana ar diviem ar atlikumu

1. solis. Nosakiet problēmu
Šajā piemērā pārvērtīsim decimālo skaitli 15610 būt binārs skaitlis. Ierakstiet decimālo skaitli kā sadalāmo skaitli apgrieztā dalījuma simbolā. Uzrakstiet mērķa numuru sistēmas bāzi (šajā piemērā “2” binārajam) kā dalījuma simbola ārpus līknes dalītāju.
- Šo metodi ir daudz vieglāk saprast, ja to uzzīmē uz papīra, un daudz vieglāk iesācējiem, jo tā dalās tikai ar diviem.
- Lai izvairītos no neskaidrībām pirms un pēc konvertēšanas, pierakstiet aprēķināto skaitļu sistēmas bāzes numuru kā apakšindeksu (mazie burti, kas rakstīti ar parastajiem burtiem kā atšķirības zīme) katram skaitlim. Šajā piemērā decimāldaļskaitļa apakšindeksam būs 10, bet binārajam - 2.

Solis 2. Veiciet sadalīšanu
Zem garā dalījuma simbola uzrakstiet veselu skaitļu atbildi (koeficientu), bet pārējo (0 vai 1) - pa labi no dalītā skaitļa.
Tā kā mēs dalām ar diviem, ja dalītais skaitlis ir pāra skaitlis, tad atlikums ir 0, un, ja dalītais skaitlis ir nepāra skaitlis, tad atlikums ir 1

Solis 3. Turpiniet dalīšanu, līdz tas sasniedz nulli
Turpiniet lejup, katru jauno koeficientu dalot ar diviem un pārējo uzrakstot pa labi no katra dalītā skaitļa. Pārtrauciet, kad koeficients ir nulle.

Solis 4. Pierakstiet jauno bināro skaitli
Sākot no mazākā atlikušā skaitļa, pārējo secību lasiet augšupejošā secībā uz augšu. Šajā piemērā jums vajadzētu iegūt rezultātu 10011100. Šis ir decimālā skaitļa 156. binārais ekvivalents. Vai, ja tas ir rakstīts ar tā ciparu bāzes apakšindeksu: 15610 = 100111002.
Šo metodi var mainīt, lai pārvērstu no decimāldaļas uz jebkuru skaitļu bāzi. Dalītājs ir 2, jo mērķa numuru sistēmas bāze ir bāze 2 (bināra). Ja galamērķa numuru sistēmas bāze ir cita bāze, nomainiet 2. bāzes numuru šajā metodē ar atbilstošo bāzes numuru. Piemēram, ja galamērķa bāze ir 9. bāze, nomainiet 2. bāzes numuru ar 9. Gala rezultāts būs tieši galamērķa bāzes numura formā
2. metode no 2: divu atvasināšana un atņemšana

1. solis. Sāciet ar tabulas izveidi
Pierakstiet abu bāzes skaitļu pilnvaras "2. tabulas bāzē" no labās uz kreiso pusi. Sāciet 20, uzrakstiet to kā “1”. Paaugstiniet rangu par 1 katrai pakāpei. Aizpildiet tabulu, līdz iegūstat skaitli, kas ir vistuvāk jūsu aprēķināto decimālo skaitļu sistēmas skaitlim. Šajā piemērā pārvērtīsim decimālo skaitli 15610 būt binārs skaitlis.

2. solis. Atrodiet skaitli ar lielāko bāzes skaitļa 2 jaudu
Tabulā izvēlieties lielāko skaitli, kas ir vienāds vai mazāks par konvertējamo. Skaitlis 128 ir skaitlis ar lielāko bāzes skaitļa 2 jaudu un ir arī mazāks par 156, tāpēc tabulā zem šī lodziņa ierakstiet skaitli "1", kur lielākais skaitlis no tabulas atrodas kreisajā pusē (sk. Tabulu attēlā iepriekš). Tad atņemiet 128 no sākotnējā skaitļa, jūs saņemsiet: 156 - 128 = 28.
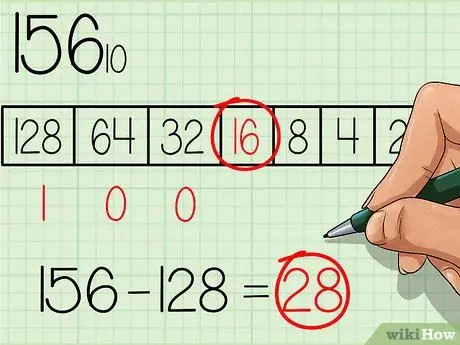
Solis 3. Pārejiet uz nākamo mazāko jaudu tabulā
Izmantojot jauno numuru (28), turpiniet skatīt tabulu no kreisās uz labo pusi, vienlaikus pārbaudot, vai skaitļi ir vienādi vai mazāki par jauno numuru. Skaitlis 64 nav mazāks par 28, tāpēc zem ciparu lodziņa 64. ierakstiet skaitli “0”. Turpiniet, līdz atrodat skaitli, kas ir vienāds vai mazāks par 28.
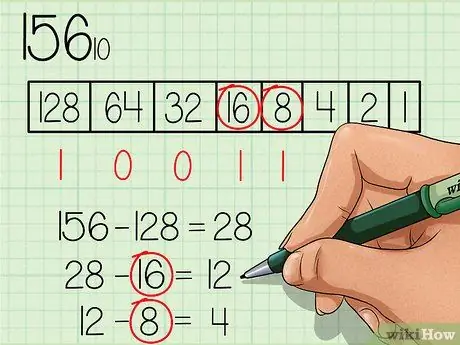
4. solis. Nepārtraukti atņemiet katru skaitli, kas ir vienāds vai mazāks par jauno, un atzīmējiet skaitli “1” zem atbilstošā skaitļa lodziņa
Skaitlis 16 ir mazāks par 28, tāpēc zem skaitļu lodziņa 16 uzrakstiet skaitli "1" un no 28 atņemiet 16, lai iegūtu jaunu skaitli 12. Skaitlis 8 ir mazāks par 12, tāpēc zemāk ierakstiet skaitli "1" skaitļu lodziņu 8 un atņemiet 8 no 12, lai iegūtu jauno skaitli 4.

5. solis. Turpiniet, līdz sasniedzat tabulas beigas
Atcerieties zem katra lodziņa atzīmēt “1”, ja skaitļi ir vienādi vai mazāki par jauno skaitli, un “0” zem katra lodziņa, ja skaitļi joprojām ir lielāki par jauno skaitli.
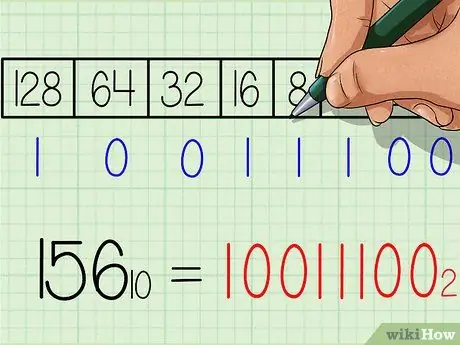
6. solis. Pierakstiet bināro skaitļu atbildi
Skaitlis no kreisās uz labo būs tieši tāds pats kā ciparu rinda “1” un “0” tabulas apakšā. Jums vajadzētu iegūt rezultātu 10011100. Šis ir decimāldaļskaitļa 156. binārais ekvivalents. Vai arī rakstot ar apakšindeksu: 15610 = 100111002.
Šīs metodes atkārtošana var palīdzēt atcerēties otrā pamata pilnvaras, lai jūs varētu izlaist 1. darbību
Padomi
- Operētājsistēmā iebūvētā kalkulatora programma var veikt šo reklāmguvumu jūsu vietā, taču kā programmētājam vislabāk ir sākt ar labu izpratni par reklāmguvumu darbību. Kalkulatora programmas konvertēšanas opcijas var padarīt redzamas, atverot izvēlni “Skatīt” un izvēloties “Programmētājs” (operētājsistēmai Windows 7 un 8).
- Vispirms ir vieglāk iemācīties konvertēt pretējā virzienā, t.i., no bināro uz decimālo skaitļu sistēmu.
- Bieži praktizējiet decimālo skaitļu pārvēršanu binārajos, lai kļūtu eksperts.






